Dynamika kmitavého pohybu
Dynamika zkoumá příčiny pohybu. Příčinou kmitání mechanického oscilátoru je buď síla pružnosti, nebo tíhová síla.
Zrychlení harmonického kmitavého pohybu je a = –ω2y.
Síla, která způsobuje harmonické kmitání, je potom F = ma = –mω2y.
Tuto rovnici označujeme jako pohybovou rovnici mechanického oscilátoru.

Obr. 1: Dynamika kmitavého pohybu
V rovnovážné poloze platí kΔl = mg (k je tuhost pružiny, Δl je prodloužení pružiny, m je hmotnost tělesa a g je tíhové zrychlení).
Jakmile oscilátor kmitá, síla pružnosti Fp se mění, ale tíhová síla FG zůstává konstantní (viz obrázek výše).
Na oscilátor (těleso) působí výsledná síla F = Fp + FG, pro velikost této síly platí:
F = k(Δl – y) – mg = kΔl – mg – ky = – ky.
Srovnáme-li získaný výsledek s pohybovou rovnicí mechanického oscilátoru:
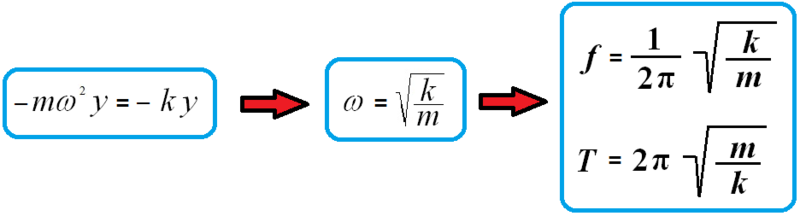
Úhlová frekvence ω volně kmitajícího mechanického oscilátoru závisí jen na jeho parametrech, tj. na hmotnosti m tělesa a tuhosti k pružiny.
Úlohy:
1. Pružinový oscilátor vznikl zavěšením tělesa o hmotnosti 0,5 kg na pružinu, která se prodloužila o 15 cm. Určete periodu a frekvenci oscilátoru (g = 9,8 m∙s-2).
2. Těleso zavěšené na pružině o tuhosti 20 N∙m-1 vykoná 40 kmitů za 50 s. Určete hmotnost tělesa.
3. Mechanický oscilátor tvořený tělesem o hmotnosti 250 g zavěšeným na pružině o tuhosti 30 N∙m-1 kmitá s amplitudou 4 cm. Určete:
a) rychlost tělesa v rovnovážné poloze
b) největší sílu, která na těleso v průběhu periody působí.
4. Mechanický oscilátor je tvořen železnou kuličkou zavěšenou na pružině. Jak se změní frekvence (perioda) kmitání oscilátoru, jestliže železnou kuličku zaměníme kuličkou hliníkovou o stejném objemu?
5. Těleso o hmotnosti 0,5 kg je zavěšeno na pružině o tuhosti 50 N∙m-1. Při kmitání tohoto oscilátoru byla měřením zjištěna perioda vlastního kmitání 0,67 s. Určete periodu výpočtem a uvažte, co může být příčinou zjištěného rozdílu. Jakou hmotnost by musel mít oscilátor, aby teoretická hodnota periody odpovídala hodnotě naměřené?
6. Změřte pomocí stopek periodu mechanického oscilátoru. (Video_1) Ze známé hmotnosti (m = 250 g) a naměřené periody vypočítejte tuhost pružiny.
7. Změřte pomocí stopek periodu mechanického oscilátoru. (Video_2) Ze známé hmotnosti (m = 100 g) a naměřené periody vypočítejte tuhost pružiny.
8. Změřte pomocí stopek periodu mechanického oscilátoru. (Video_3) Ze známé hmotnosti (m = 200 g) a naměřené periody vypočítejte tuhost pružiny.
9. Pomocí programu pro videoanalýzu (např. program Logger Pro) proveďte analýzu kmitavých pohybů z předcházejících úloh.
10. Položíme-li na pružinové závěsné kuchyňské váhy dva kilogramové balíčky soli, poklesne miska o 1,2 cm. Jaká je tuhost pružiny? S jakou periodou bude miska kmitat? Skutečná perioda kmitů bude kratší nebo delší?
11. Ponoříme-li hustoměr do kapaliny, bude kmitat. Jde o kmity harmonické? Dokažte to. Např. pomocí videoanalýzy.
