Hurwitzovo kritérium

Hurwitzovo kritérium stability patří mezi algebraická kritéria – řeší se výpočtem.

Vychází z charakteristické rovnice zkoumaného obvodu. Posuzuje to, jestli je nebo není obvod stabilní, ale nelze určit, jak dalece je obvod stabilní. Není použitelné v obvodech s dopravním zpožděním.

Při jeho použití nejprve zkontrolujeme nutnou podmínku stability: všechny koeficienty charakteristické rovnice musí být nenulové se stejným znaménkem.

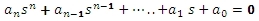
Pokud je n>2, sestavíme Hurwitzův determinant D_H stejného řádu, jako je stupeň rovnice. Pro n=5 například takto:

Definice: Obvod je podle Hurwitzova kritéria stabilní, jsou-li všechny subdeterminanty až do řádu (n-1) kladné nenulové.

Pokud je subdeterminant (n-1) roven nule, je obvod na mezi stability.

Úloha 1.

Rozhodněte pomocí Hurwitzova kritéria o stabilitě obvodu s charakteristickou rovnicí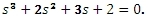

Nutná podmínka stability je splněna, sestavíme Hurwitzův determinant.

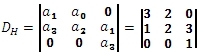
Vypočteme subdeterminanty:

Δ₁ = a₁ = 3>0

Δ₂ = a₁a₂ – a₀a₃ =3·2 - 2·1 = 4>0

Závěr: Obvod je stabilní.

Úloha 2.

Zkontrolujte stabilitu regulačního obvodu s charakteristickou rovnicí

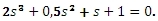
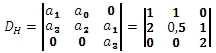
Δ₁ = a₁ = 1>0

Δ₂ = a₁a₂ – a₀a₃ =1·0,5 - 2·1 = -1,5<0

Závěr: Obvod je nestabilní.

Úloha 3.

Zkontrolujte stabilitu Hurwitzovým kritériem, je-li přenos řízení obvodu:

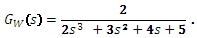
Výsledek: Obvod je stabilní.