Odraz a lom vlnění

Jestliže mechanické vlnění dopadne na rozměrnou překážku, může se odrážet. Jestliže mechanické vlnění dopadne na rozhraní mezi dvěma prostředími, v nichž se vlnění šíří různou rychlostí, potom nastává lom vlnění. Huygensův princip použijeme k výkladu těchto dějů.

Odraz vlnění

Obr. 1: Odraz vlnění

Obr. 2: Odraz vlnění znázorněný pomocí Huygensova principu

Pro odraz vlnění platí zákon odrazu:

Úhel odrazu vlnění se rovná úhlu dopadu: α´ = α

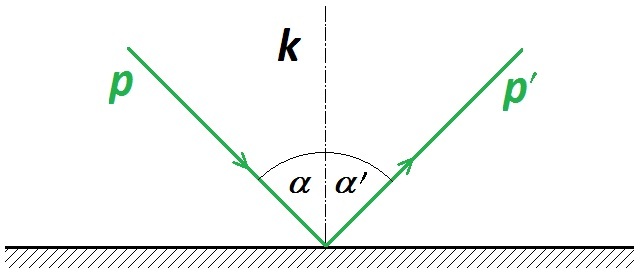
Obr. 3: Zákon odrazu znázorněný pomocí paprsků

Dopadající vlnění je vyznačeno paprskem p, který svírá úhel dopadu α s kolmicí (kolmice dopadu k). Paprsek p´ odraženého vlnění svírá s kolmicí dopadu úhel odrazu α´. Rovina určená kolmicí dopadu a dopadajícím paprskem je rovina dopadu. Platí, že odražený paprsek zůstává v rovině dopadu.

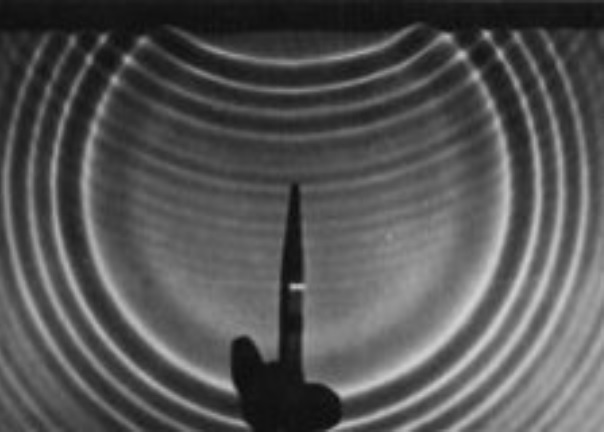
Obr. 4: Odraz vlnění z bodového zdroje

Lom vlnění

Jestliže mechanické vlnění dopadne na rozhraní mezi dvěma prostředími, v nichž se vlnění šíří různou rychlostí, potom nastává lom vlnění. Předpokládáme, že rychlost vlnění v prvním prostředí je v₁ a ve druhém prostředí v₂ (v₁ ˃ v₂). Kde α je úhel dopadu a β je úhel lomu vlnění (viz horní část obr. 5).

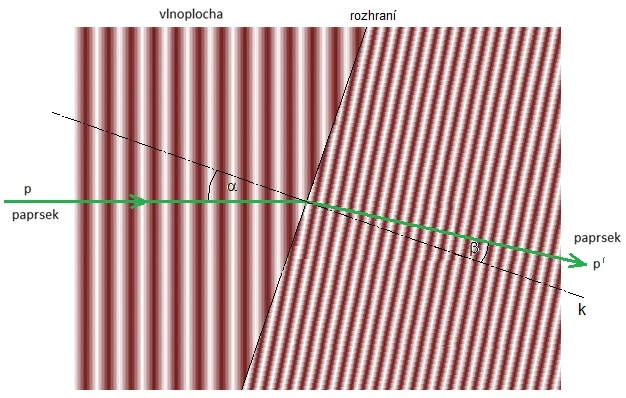
Obr. 5: Lom vlnění

Jestliže je β < α, nastává lom ke kolmici (v₁ ˃ v₂). Jestliže je β ˃ α, nastává lom od kolmice (v₁ < v₂).

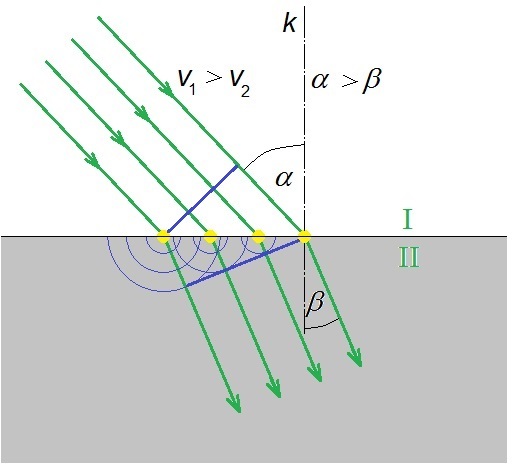
Obr. 6: Lom vlnění znázorněný pomocí Huygensova principu

Pro lom vlnění platí zákon lomu vlnění (Snellův zákon - viz historická poznámka):

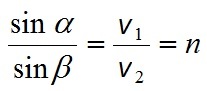
v₁…rychlost vlny v prvním prostředí

v₂…rychlost vlny ve druhém prostředí

n…index lomu

α…úhel dopadu

β…úhel lomu

Lom mechanického vlnění většinou nepozorujeme. Mnohem větší význam má lom světla. Budeme se jím zabývat v optice.

Úlohy:

1. Vypočítejte úhel lomu, jestliže úhel dopadu je 20 ° a index lomu je 1,33. Nastává „lom ke kolmici“ nebo „lom od kolmice“?

2. Vypočítejte úhel lomu, jestliže úhel dopadu je 40 ° a rychlost vlnění v prvním prostředí (látce) je 3 m∙s^-1 a ve druhém prostředí (látce) je 4 m∙s^-1. Nastává „lom ke kolmici“ nebo „lom od kolmice“?