Regulované soustavy

Obr. 1: Regulovaná soustava
Regulované soustavy svými přenosovými vlastnostmi nejvíce ovlivňují průběh regulačního procesu. Při návrhu regulace potřebujeme přenosové regulované soustavy znát, abychom mohli zvolit vhodný typ a seřízení regulátoru.
Regulované soustavy mohou mít charakter některého typového členu uvedeného v předchozích lekcích, kromě derivačního členu. Rozlišujeme regulované soustavy statické a astatické.
Statické regulované soustavy mají tu vlastnost, že po změně akční veličiny se regulovaná veličina po odeznění přechodného děje ustálí bez působení regulátoru (autoregulace). Rozdělení podle řádu setrvačnosti, diferenciální rovnice, přiřazení k typovému členu a příklad uvádí následující tabulka:
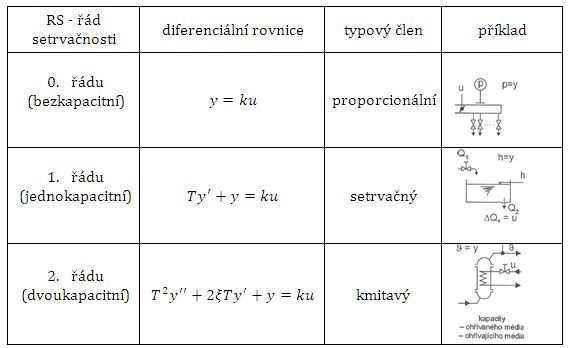
Obr. 2: Statické regulované soustavy
Astatické regulované soustavy jsou soustavy, u kterých při změně akční veličiny regulovaná veličina trvale klesá nebo stoupá. Jsou méně časté než statické soustavy:
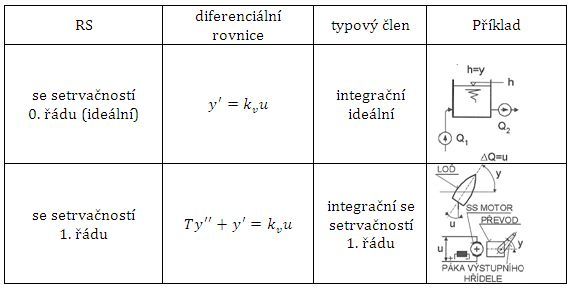
Obr. 3: Astatické regulované soustavy
Obecně platí, že čím je řád soustavy vyšší, tím je regulace obtížnější a že statické soustavy se regulují lépe než astatické.
Kromě uvedených vlastností mohou mít soustavy všech typů ještě dopravní zpoždění τ, které je způsobeno konečnou rychlostí šíření signálu v soustavě a projeví se zpožděním výstupního signálu vzhledem k časovému působení vstupního signálu. Jako příklad členu s dopravním zpožděním může sloužit pásový dopravník, který způsobuje dopravní zpoždění
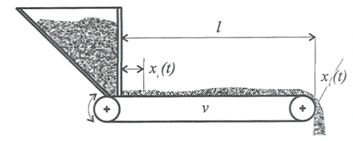
Obr. 4: Pásový dopravník jako člen s dopravním zpožděním
Účinek dopravního zpoždění je stejný, jako by se o hodnotu τ zpožďoval vstupní signál, takže např. statickou regulovanou soustavu 0. řádu s dopravním zpožděním popíšeme diferenciální rovnicí:
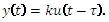
V Laplaceově transformaci při posunutí časové funkce násobíme její obraz výrazem e-sτ :
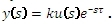
Obrazový přenos má tvar:
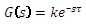
a frekvenční přenos je
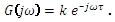
Dopravní zpoždění tedy způsobí posunutí přechodové charakteristiky o úsek τ. Z frekvenčního přenosu vyplývá, že roste fázový úhel a soustava se chová jako soustava vyššího řádu bez dopravního zpoždění.
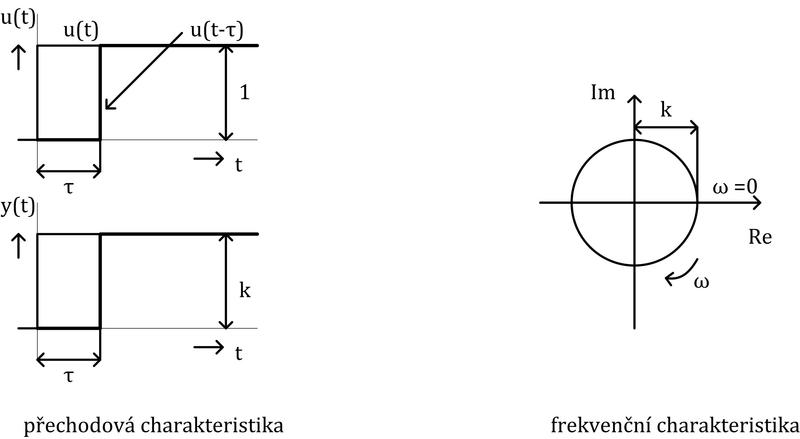
Obr. 5: Charakteristiky statické soustavy 0. řádu s dopravním zpožděním
Dopravní zpoždění je v regulačních obvodech nežádoucí, protože soustava není po dobu τ řízena.
Zjištění přenosových vlastností soustavy označujeme jako její identifikaci. Můžeme změřit přechodovou charakteristiku nebo pro jednoduché regulované soustavy sestavit diferenciální rovnici a přenos vypočítat. Pokud vlastnosti skutečné soustavy neodpovídají některému typovému členu, provedeme vhodnou metodou náhradu aproximací.


