Měření hustoty tělesa pomocí Archimédova zákona

Měření hustoty tělesa pomocí Archimedova zákona

Teoretická příprava

V této laboratorní úloze si vyzkoušíme určit hustotu kvádru, a to hned třemi způsoby. Na základě měření délek hran kvádru délkovým měřidlem, měřením objemu kvádru odměrným válcem a měřením vztlakové síly.

Střední hodnoty délek hran a₀, b₀, c₀ použijeme pro výpočet objemu kvádru:

$V=a_{0}b_{0}c_{0}$

Střední hodnota vyjadřuje aritmetický průměr naměřených veličin:

$a_{0}=\frac{a_{1}+a_{2}+...+a_{n}}{n}$

Hustotu pevné látky, ze které je kvádr složený, vypočítáme ze vztahu:

$\rho =\frac{m}{V_{0}}$

kde m je hmotnost kvádru.

Hustotu tělesa převedeme na jednotky kg/m³ podle vztahu:

$1 g/cm^{3}=1000 kg/m^{3}$

Hustotu kvádru můžeme ještě určit jiným způsobem pomocí Archimedova zákona. Archimedův zákon, který objevil řecký filosof a učenec Archimédés ve 3.stol.př.n.l., zní : „Těleso zcela ponořené do kapaliny je nadlehčováno silou, která se rovná tíze kapaliny tělesem vytlačené.“ Skutečnost, že těleso zcela ponořené do kapaliny vytlačí kapalinu stejného objemu jako těleso samé, můžeme využít k určení objemu tělesa. Změříme-li objem kapaliny V₁ v odměrném válci a objem kapaliny V₂ po ponoření kvádru do válce, pak rozdíl objemů je objem kvádru:

$V=V_{1}-V_{2}$

a hustota je pak:

$\rho =\frac{m}{V}$

Síla, kterou je těleso v kapalině nadlehčováno se nazývá vztlaková.

Jestliže změříme tíhovou sílu F₁, kterou působí Země na pevné těleso ve vzduchu a potom tíhovou sílu F₂ působící na těleso zcela ponořené do kapaliny, pak pro velikost vztlakové síly platí vztah:

$F_{vz}=\rho _{k}.V.g=F_{1}-F_{2}$

Velikost sil F₁, F₂ změříme pomocí siloměru.

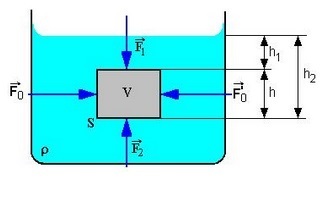Obr. 1: Síly působící na těleso v kapalině

odtud pro objem tělesa platí:

$V=\frac{F_{1}-F_{2}}{\rho _{k}.g}$

Po dosazení do vztahu:

$\rho =\frac{m}{V}$

dostaneme pro hustotu tělesa:

$\rho =\frac{\rho _{k}.g.m}{F_{1}-F_{2}}$

kde ρ_k je hustota vody, g je tíhové zrychlení a m je hmotnost kvádru v kilogramech.

Pomůcky

Kvádr, délkové měřidlo, odměrný válec s vodou, digitální váha, fyzikální tabulky, modul siloměr, chemický stojan, svorky, ISES.

Obr. 2: Sestavení pokusu

Postup práce

Zvážíme kvádr pomocí digitální váhy.
Změříme délky hran kvádru a, b, c délkovým měřidlem a zapíšeme hodnoty do tabulky.
Vypočítáme střední hodnoty délek hran.
Vypočítáme objem kvádru.
Vypočítáme hustotu kvádru.
Nalijeme do odměrného válce tolik vody, aby byl kvádr ve válci zcela ponořen.
Změříme objem vody ve válci V₁.
Zcela ponoříme kvádr do vody ve válci a změříme objem vody ve válci V₂.
Vypočítáme přírůstek objemu vody ve válci V.
Vypočítáme hustotu kvádru.
K chemickému stojanu připevníme modul siloměr na určení sil F₁, F₂.

Na siloměr zavěsíme pomocí tenkého drátu nebo niti pevné těleso.Obr. 3: Modul siloměr
Změříme tíhovou sílu F₁ působící na pevné těleso na vzduchu.
Pevné těleso zcela ponoříme do vody a opět změříme siloměrem tíhovou sílu F₂ působící na těleso.Obr. 4: Určení tíhové síly působící na těleso v kapalině

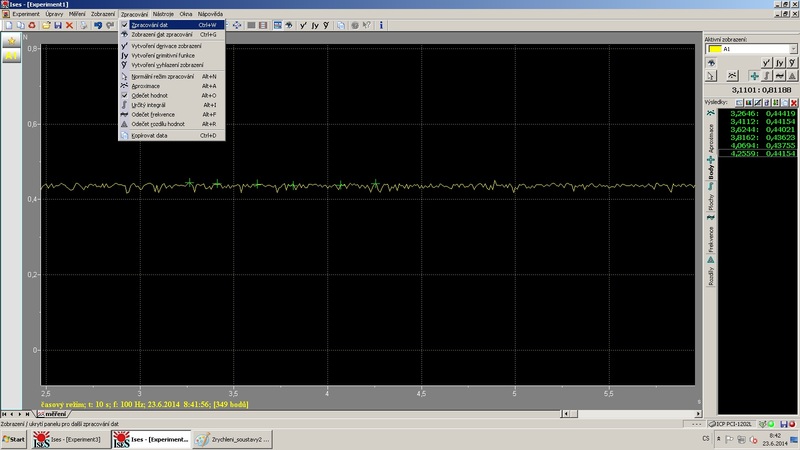Obr. 5: Odečtení hodnot z grafu

Vypočítáme hustotu pevného tělesa.
Naměřenou hustotu porovnáme s hustotou ve fyzikálních tabulkách.

Zdroje

Archimédés. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2014-11-13]. Dostupné z: http://cs.wikipedia.org/wiki/Archim%C3%A9d%C3%A9s
Archimédův zákon. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2014-11-29]. Dostupné z: http://cs.wikipedia.org/wiki/Archim%C3%A9d%C5%AFv_z%C3%A1kon#Historick.C3.A1_pozn.C3.A1mka
Archimédés. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2014-11-29]. Dostupné z: http://cs.wikipedia.org/wiki/Archim%C3%A9d%C3%A9s#mediaviewer/File:Archimedes_water_balance.gif
Archimédův zákon. Www.zsondrejov.cz: Základní a mateřská škola bratří Fričů Ondřejov [online]. 2014 [cit. 2014-11-29]. Dostupné z: http://www.zsondrejov.cz/Vyuka/F-8/Kapal_05.pdf
Vztlaková síla. Vztlaková síla [online]. 2009 [cit. 2014-11-29]. Dostupné z: https://www.youtube.com/watch?v=VpwZv_2QLkQ
Karteziánek. Populární fyzika [online]. 2012 [cit. 2014-11-29]. Dostupné z: http://www.popularni-fyzika.cz/pokus/kartezianek
Archimédův zákon. Učitel.net - tvoje online škola [online]. 2010-2014 [cit. 2014-11-29]. Dostupné z: http://www.ucitel.net/fyzika/archimeduv-zakon
Podpora výuky fyziky a chemie formou prezentace. Podpora výuky fyziky a chemie formou prezentace [online]. 2006 [cit. 2015-01-16]. Dostupné z: http://www.prezentace-fyzika-chemie.wz.cz/fyzika.html

Obrázky:

Obr. 1: BÁRTA, Ivo. Archimedův zákon [online]. ČR, 2006 [cit. 2014-11-09]. Dostupné z: http://archimeduvzakon.chytrak.cz/paragraph.html. Školní práce.
Obr. 2: archiv autora
Obr. 3: archiv autora
Obr. 4: archiv autora
Obr. 5: archiv autora

Přílohy

Archimeduv_zakon.docx Stáhnout

Protokol

Laboratorní protokol najdete zde.

Historie

Kdo byl Archimédés?

Víte, že ...

... Archimédův objev byl inspirován problémem odhalení podvodného klenotníka, který šidil královu zlatou korunu stříbrem? Koruna měla větší objem, než objem zlata vážícího stejně jako koruna. Proto byla nadlehčována po ponoření do vody větší silou než zlato.