Fáze kmitavého pohybu

Těleso nemusí své kmitání začít v rovnovážné poloze. Říkáme, že má počáteční fázi φ₀. Počáteční fáze může mít kladnou nebo zápornou hodnotu (viz obr. 1).

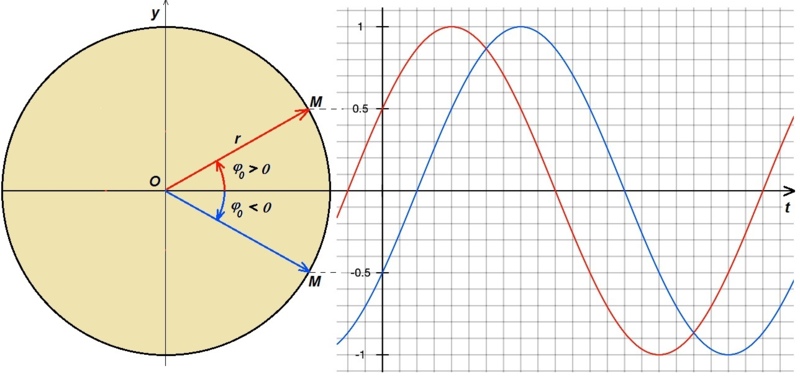
Obr. 1: K výkladu počáteční fáze

y = y_m sinω(t + t₀) = y_m sin(ωt + ωt₀) = y_m sin(ωt + φ₀)

φ₀…počáteční fáze

Otestuj se →

! Fázový rozdíl dvou harmonických veličin o stejné frekvenci je určen rozdílem jejich počátečních fází.

Fázový rozdíl je důležitou veličinou pro posouzení vzájemných vztahů fyzikálních veličin. Nejvýznamnější jsou tyto případy:

a) kmitání se stejnou fází:

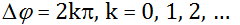
Obr. 2: Kmitání se stejnou fází

b) kmitání s opačnou fází:

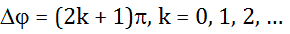
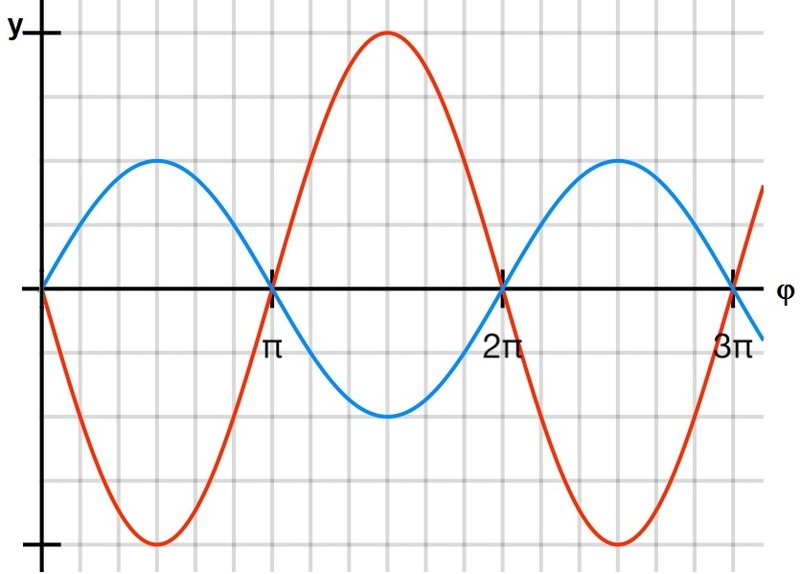
Obr. 3: Kmitání s opačnou fází

Úlohy:

1. Mechanický oscilátor byl v rovnovážné poloze v čase t = T/8. Určete počáteční fázi kmitání a napište rovnici výchylky oscilátoru.

2. Dva mechanické oscilátory kmitají harmonicky se stejnou frekvencí tak, že v počátečním okamžiku mají výchylku 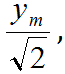ale pohybují se opačným směrem. Určete počáteční fázi a fázový rozdíl kmitání oscilátorů.

3. Nakreslete časové diagramy dvou harmonických kmitavých pohybů

a) se stejnou fází,

b) s opačnou fází.

4. Napište rovnice výchylek harmonického kmitání z úlohy 3, jestliže počáteční fáze jednoho z pohybů je – π/2.

5. Mechanický oscilátor harmonicky kmitá podle vztahu y = y_mcos(ωt +φ₀). Určete počáteční fázi kmitání, jestliže v počátečním okamžiku (t=0) je výchylka oscilátoru

a) – y_m

b) 0

c) y_m/2.