Rovnice postupného vlnění

Okamžitá výchylka kmitajícího bodu je jen funkcí času y = y_m sin ωt.

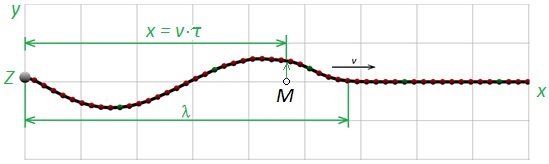
Obr. 1: K odvození rovnice postupné vlny (τ - doba za kterou dospěje vlnění od zdroje Z do bodu M)

Upravením rovnice pro kmitání částice v bodě M (obr. 1) dostaneme rovnici postupné vlny pro příčné i podélné vlnění v homogenním prostředí:

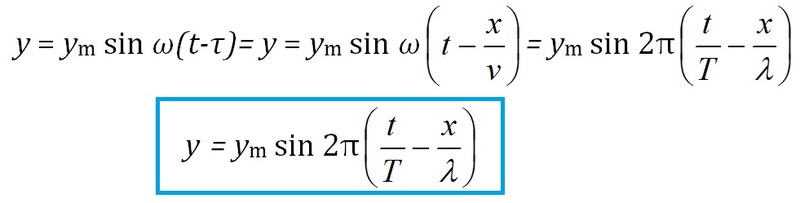
Všechny veličiny popisující vlnění jsou jak funkcemi času, tak funkcemi polohy (souřadnice) bodu, kterým vlnění prochází.

Úlohy:

1. Příčné vlnění s vlnovou délkou 30 cm postupuje řadou bodů. Zdroj vlnění kmitá s amplitudou 4 cm a s frekvencí 4 Hz. Napište:

a) rovnici postupné vlny,

b) rovnici kmitavého pohybu pro bod vzdálený 10 cm od zdroje vlnění.

2. Postupné mechanické vlnění je popsáno rovnicí {y} = 0,1 sin 2π(5{t} – 3,3{x}). Určete amplitudu, vlnovou délku a rychlost vlnění.

3. Zdroj vlnění kmitá s frekvencí 0,2 Hz a s amplitudou 4 cm. V počátečním okamžiku má nulovou výchylku i počáteční fázi. Určete výchylku bodu vzdáleného 40 cm od zdroje v čase 10 s od počátečního okamžiku, jestliže vlnová délka vlnění je 50 cm. Napište rovnici postupné vlny.

4. Jaký tvar bude mít rovnice postupné vlny, jestliže počáteční fáze zdroje vlnění není nulová, ale má hodnotu π/4?