Elektronická učebnice

Zobrazení dutým zrcadlem

Zrcadlící plochu kulových zrcadel tvoří část povrchu koule (kulový vrchlík).

Odráží-li světlo vnitřní část kulové plochy, jedná se o duté kulové zrcadlo, pokud světlo odráží vnější část kulového vrchlíku, jde o vypuklé kulové zrcadlo.

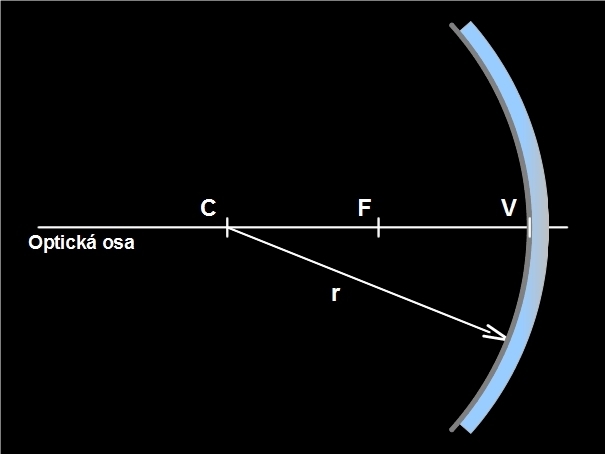
obrazek

Obr. 1: Vyznačení základních pojmů u dutého zrcadla

Pro oba typy kulových zrcadel zavádíme tyto pojmy:

střed křivosti C – střed kulové plochy, jejíž částí je zrcadlící plocha

vrchol zrcadla V

optická osa zrcadla o – přímka procházející středem křivosti C a vrcholem zrcadla V

poloměr křivosti zrcadla r – vzdálenost CV

osový bod – bod ležící na optické ose

ohnisko F – obraz předmětového osového bodu, který leží velmi daleko od zrcadla, teoreticky v nekonečnu. Ohnisko F je středem úsečky CV.

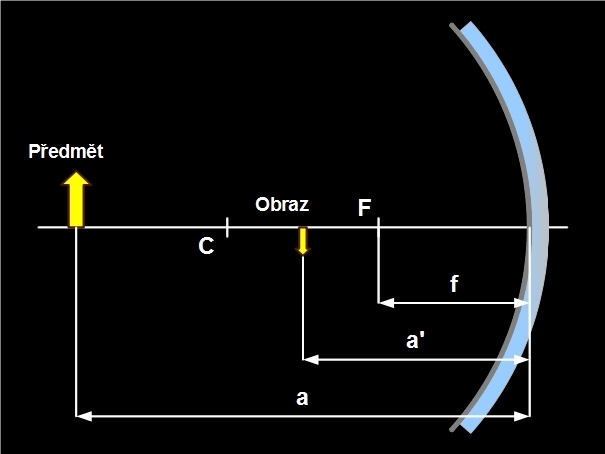
obrazek

Obr. 2: Duté zrcadlo – popis vzdáleností

ohnisková vzdálenost f – vzdálenost ohniska F od vrcholu V, fyzikální veličina definovaná vztahem $\left | CF \right |=\left | FV \right |=\frac{r}{2}=f$ , její jednotkou je metr

předmětová vzdálenost a – vzdálenost zobrazovaného bodového předmětu, který leží na optické ose od vrcholu zrcadla

obrazová vzdálenost a´ – vzdálenost obrazu od vrcholu zrcadla

V dalších úvahách se omezíme jen na paprsky, které se nacházejí v blízkosti optické osy, kterými se bod zobrazuje jako bod, přímka jako přímka. Tyto paprsky označujeme jako paraxiální.

Paraxiální prostor je prostor v blízkosti optické osy, ve kterém se zobrazení uskutečňuje paraxiálními paprsky. Lze jej definovat také jako prostor, ve kterém dopadají paprsky na zrcadlo pod malými úhly. V tomto prostoru je optické zobrazení ideální, při zobrazování nevznikají žádné vady. U většiny používaných kulových zrcadel je paraxiálnost zajištěna tím, že zrcadlo představuje malou část kulové plochy, ze které je zhotoveno.

Geometrická konstrukce obrazu

Libovolný paprsek, který dopadá na odraznou plochu dutého zrcadla, se odráží podle zákona odrazu. Při optickém zobrazení dutým zrcadlem je vhodné použít pro geometrickou konstrukci obrazu tři význačné paprsky:

Paprsek procházející středem křivosti má po odrazu na zrcadle opačný směr, než měl před dopadem na zrcadlo, tj. odráží se zpět do středu křivosti C. Tento paprsek dopadá na odraznou plochu kolmo a dle zákona odrazu se odráží zpět.

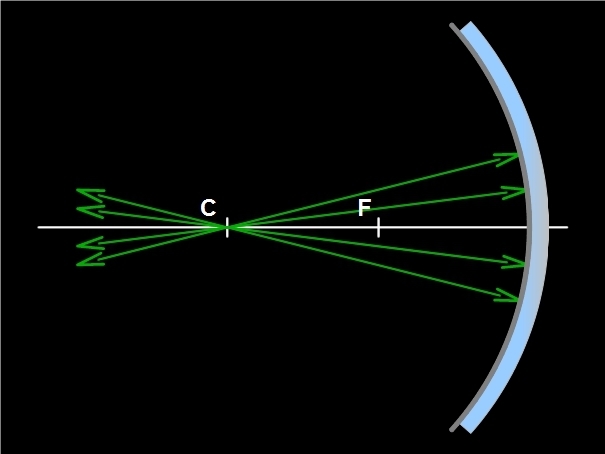
obrazek

Obr. 3: Paprsky jdoucí středem křivosti

Paprsek rovnoběžný s optickou osou zrcadla podle zákona odrazu mění svůj směr a odráží se do ohniska F. Jedná se o paprsek z velmi vzdáleného zdroje světla. U dutého zrcadla se tyto paprsky v ohnisku skutečně protínají, ohnisko F dutého zrcadla je skutečné.

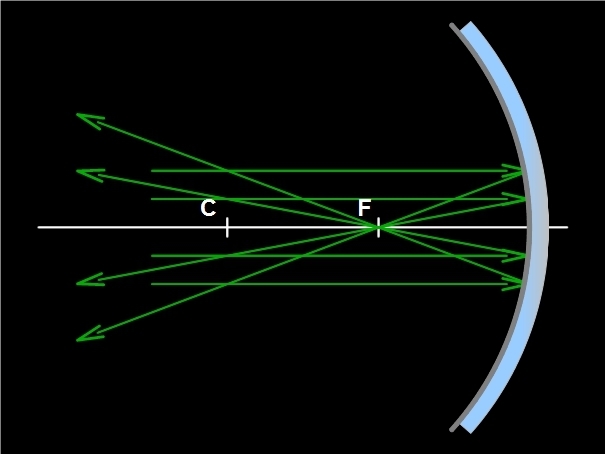
obrazek

Obr. 4: Paprsky rovnoběžné s optickou osou

Paprsek procházející ohniskem se odráží rovnoběžně s optickou osou zrcadla.

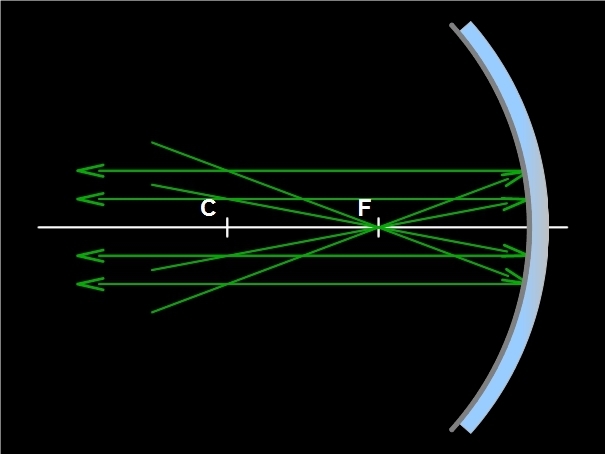
obrazek

Obr. 5: Paprsky procházející ohniskem

Pro geometrickou konstrukci obrazu stačí využít dva význačné paprsky. Dále využíváme poznatku, že obrazem bodu, který leží na optické ose, je opět bod na optické ose. Při jednotlivých konstrukcích obrazu znázorňujeme předmět šipkou kolmou k optické ose.

Z koncového bodu šipky, která znázorňuje předmět, vedeme dva význačné paprsky. V bodě, kde se paprsky po odrazu protínají, vzniká obraz.

Je-li předmětová vzdálenost větší než poloměr křivosti, duté zrcadlo vytváří skutečný, převrácený a zmenšený obraz.

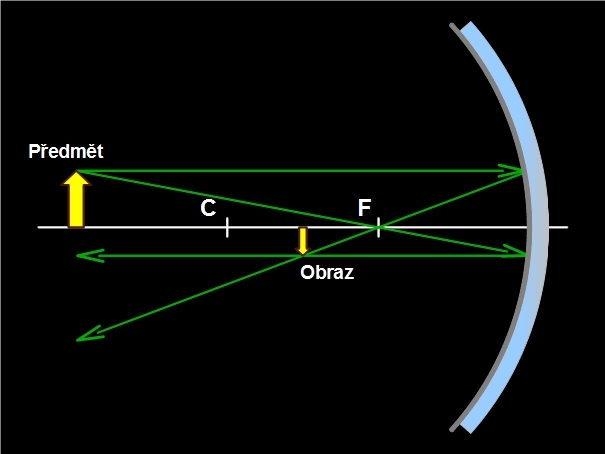
obrazek

Obr. 6: Skutečný zmenšený obraz

Leží-li předmět mezi středem křivosti a ohniskem, je vytvořený obraz skutečný, převrácený a zvětšený.

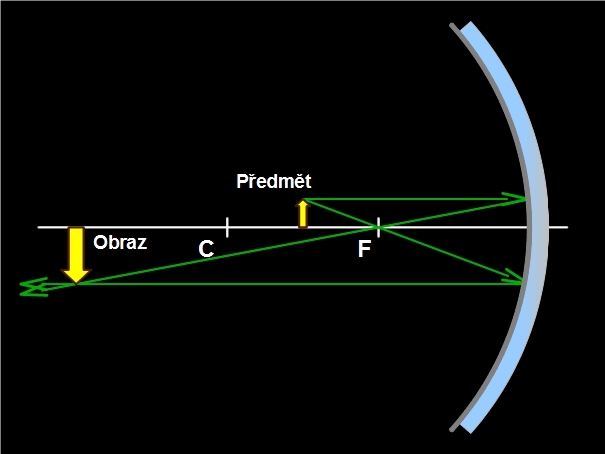
obrazek

Obr. 7: Skutečný zvětšený obraz

Umístíme-li předmět mezi ohnisko a vrchol dutého zrcadla, vytváří paprsky odražené na dutém zrcadle rozbíhavý svazek. Odražené paprsky zpětně prodloužíme, v průsečíku zpětně prodloužených paprsků za zrcadlem vzniká obraz. Získáme obraz zdánlivý, přímý a zvětšený.

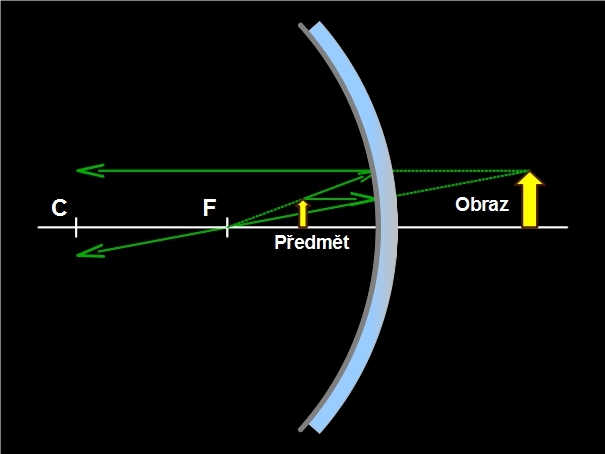
obrazek

Obr. 8: Zdánlivý zvětšený obraz

obrazek

Obr. 9: Zdánlivý a zvětšený obraz v dutém zrcadle

Kam je třeba umístit předmět, abychom získali stejně velký obraz?

Tato situace nastane, jestliže předmět leží ve středu křivosti, což geometrickou konstrukcí snadno dokážete.

Vidíme, že vlastnosti obrazu vytvořeného dutým zrcadlem závisí na poloze předmětu před zrcadlem.

Zobrazovací rovnice kulového zrcadla

Mezi vzdáleností předmětu a a vzdáleností obrazu a´ od vrcholu kulového zrcadla a ohniskovou vzdáleností f je vzájemná souvislost, kterou vyjadřuje zobrazovací rovnice kulového zrcadla:

$\frac{1}{a}+\frac{1}{{a}'}=\frac{1}{f}$

Pro danou předmětovou vzdálenost a dané zrcadlo určuje jednoznačně obrazovou vzdálenost, tedy polohu obrazu. Při dosazování do rovnice se však musíme řídit znaménkovou konvencí (dohodou).

Veličiny a, a´, f, r mají v prostoru před zrcadlem kladnou hodnotu, za zrcadlem hodnotu zápornou. Jelikož střed křivosti i ohnisko dutého zrcadla leží na optické ose před zrcadlem, mají poloměr křivosti r i ohnisková vzdálenost f dutého zrcadla kladnou hodnotu. Kladná hodnota obrazové vzdálenosti a' znamená, že obraz je skutečný, zatímco záporná hodnota a' charakterizuje obraz zdánlivý.

a´ > 0... skutečný obraz, před zrcadlem
a´ < 0... zdánlivý obraz, za zrcadlem

Pro popis dalších vlastností obrazu zavádíme veličinu příčné zvětšení Z, definované vztahem:

$Z=\frac{{y}'}{y}$

kde y' je výška obrazu, y je výška předmětu. Výšky předmětu a obrazu do něj dosazujeme s kladným znaménkem, jsou-li nad optickou osou. Zápornou hodnotu mají pod optickou osou. Pomocí veličin a, a' můžeme příčné zvětšení určit ze vztahu:

$Z=-\frac{{a}'}{a}$