V optice má velký význam zobrazení lomem, které se uskutečňuje čočkami.

Čočka je průhledné stejnorodé těleso, které je ohraničeno dvěma hladkými kulovými plochami nebo kulovou a rovinnou opticky hladkou plochou. Čočky se zhotovují ze skla nebo plastické hmoty. Index lomu materiálu čočky (značíme ) je větší než index lomu okolního prostředí (značíme ). Tvary čoček závisí na vzdálenosti středů křivosti lámavých ploch a hodnotách jejich poloměrů. Různé vztahy mezi těmito veličinami vedou k šesti základním možnostem tvarů čoček, které jsou zachyceny na obrázku.

Podle uspořádání ploch rozlišujeme spojné čočky, stručně spojky, a rozptylné čočky, rozptylky. Spojné čočky jsou uprostřed širší než na okrajích, rozptylné jsou uprostřed nejtenčí. Ve schematických nákresech používáme pro zakreslení čoček schematické značky.

Obr. 1: Tvary spojek a schematická značka

 

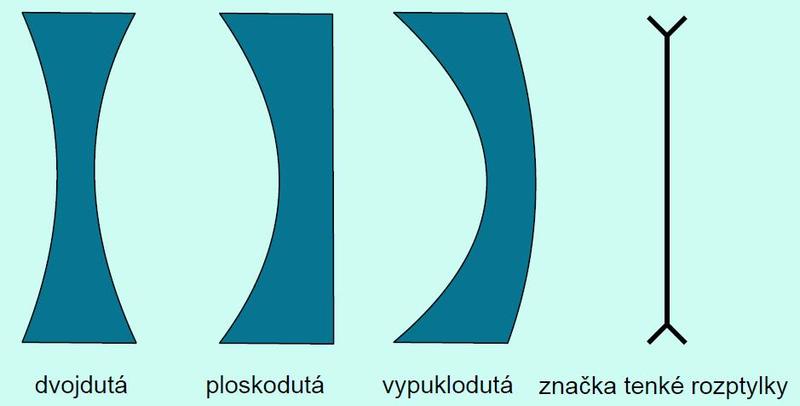
Obr. 2: Tvary rozptylek a schematická značka

 

Obr. 3: Čočky

 

Pro popis čoček jsou důležité následující pojmy:

středy optických ploch ,  – středy kulových ploch, které ohraničují čočky

poloměry křivosti optických ploch 

optická osa čočky o – přímka procházející středy , 

vrcholy čočky  – průsečíky optické osy s optickými plochami

optický střed čočky O – střed úsečky 

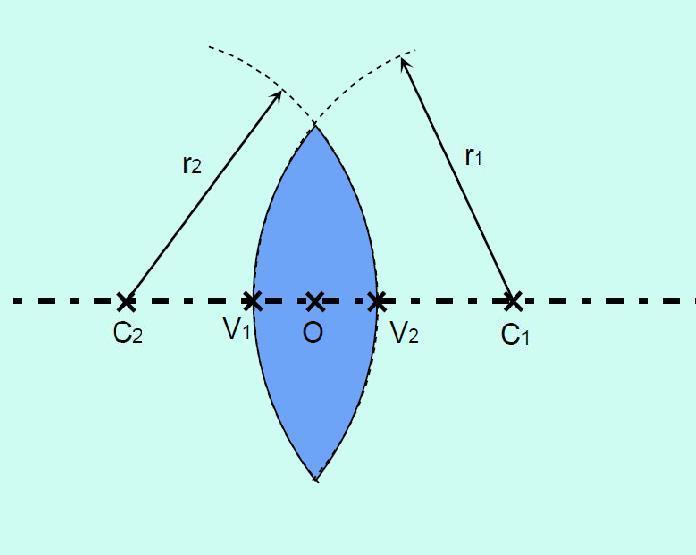
Obr. 4: Vyznačení základních pojmů u spojky

 

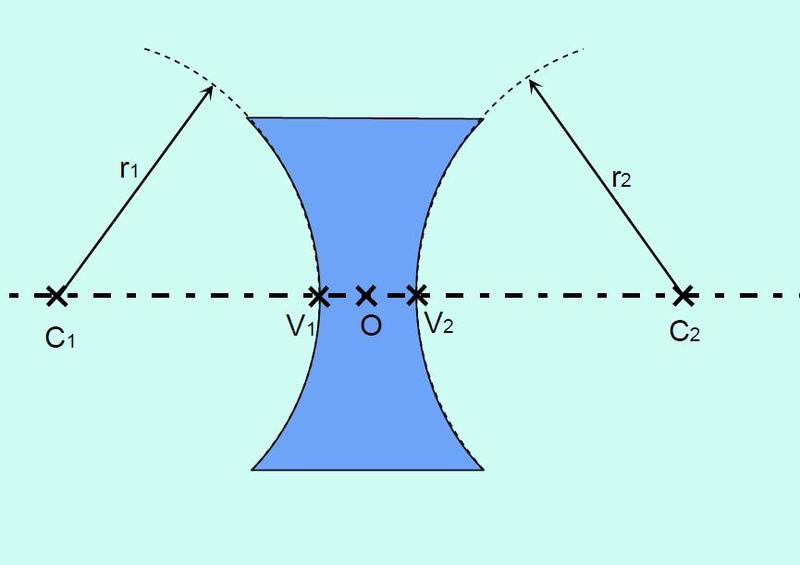
Obr. 5: Vyznačení základních pojmů u rozptylky

 

Tloušťka čočky je vzdálenost jejích vrcholů. Čočky, jejichž tloušťka je malá a lze ji vzhledem k poloměrům optických ploch zanedbat, jsou tenké čočky. U tenkých čoček body

, O splynou v jeden a tvoří optický střed čočky O.

V dalších úvahách se budeme zabývat jen tenkými čočkami.

Čočky zobrazují v důsledku zákona lomu světla na dvou rozhraních. Světlo čočkou prochází, a proto rozlišujeme:

• předmětový prostor – prostor, ze kterého světlo do čočky vstupuje (zpravidla se zakresluje zleva),

• obrazový prostor – prostor, do kterého světlo po průchodu čočkou vystupuje (zpravidla doprava).

Název spojné čočky vychází z poznatku, že paprsky rovnoběžné s optickou osou v předmětovém prostoru se po průchodu čočkou lámou (spojují) do bodu na optické ose, který nazýváme obrazové ohnisko F'. U spojky se tyto paprsky v obrazovém prostoru protínají, obrazové ohnisko je skutečné. Tuto skutečnost si můžete ověřit známým pokusem. Soustředíme-li sluneční paprsky, které můžeme považovat za rovnoběžné, spojnou čočkou do ohniska, je jejich energie dostatečná k zapálení papíru.

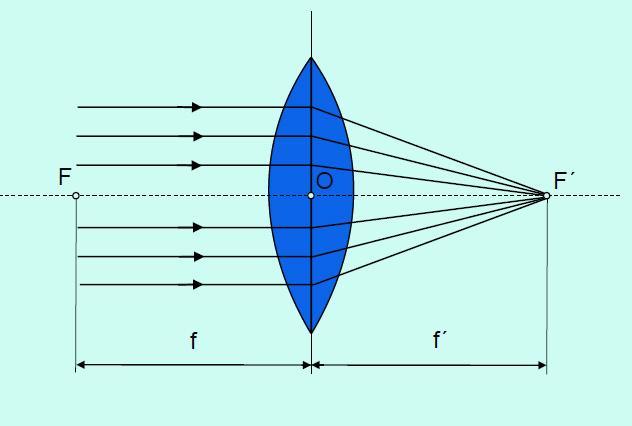
Obr. 6: Obrazové ohnisko spojky

 

U rozptylky se naopak rovnoběžné paprsky po průchodu čočkou rozbíhají a jejich průsečík najdeme zpětným prodloužením v předmětovém prostoru, obrazové ohnisko rozptylky je tedy zdánlivé.

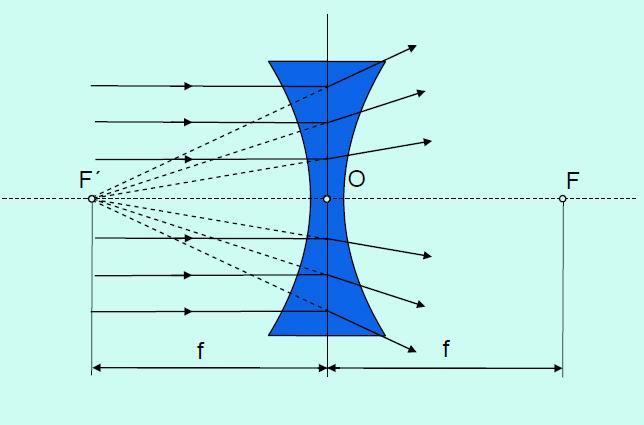
Obr. 7: Obrazové ohnisko rozptylky

 

Druhé ohnisko má spojná čočka na optické ose v předmětovém prostoru a paprsky, které vycházejí z předmětového ohniska F, jsou po průchodu čočkou rovnoběžné s optickou osou v obrazovém prostoru.

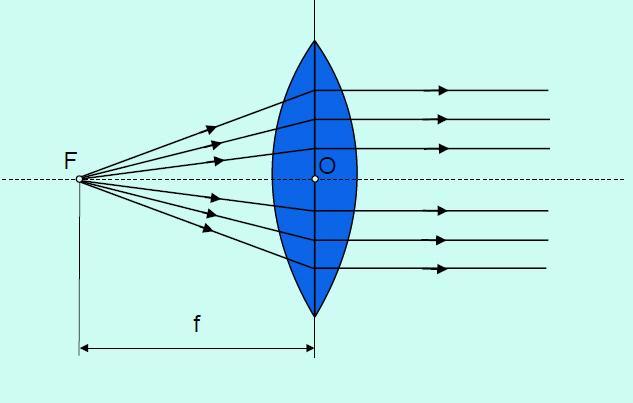
Obr. 8: Předmětové ohnisko spojky

 

U rozptylky leží předmětové ohnisko v obrazovém prostoru a paprsky, které míří do zdánlivého předmětového ohniska, jsou po průchodu rozptylkou rovnoběžné s optickou osou.

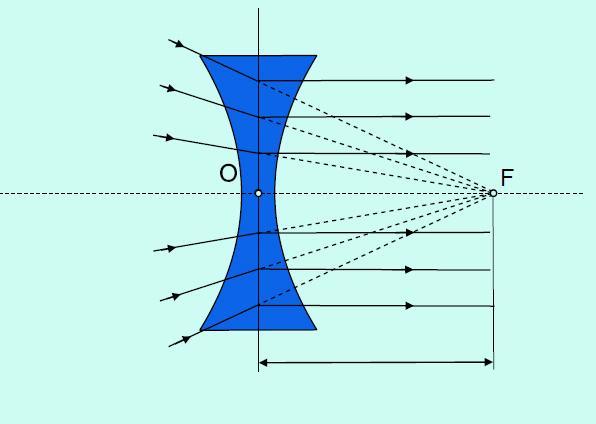
Obr. 9: Předmětové ohnisko rozptylky

 

Vzdálenost předmětového ohniska od optického středu čočky nazýváme předmětová ohnisková vzdálenost f. Vzdálenost obrazového ohniska od optického středu čočky je obrazová ohnisková vzdálenost f´. Je-li před tenkou čočkou i za ní stejné prostředí, jsou tyto vzdálenosti stejné, a proto používáme společné označení ohnisková vzdálenost čočky f. Její hodnota závisí na indexech lomu materiálu čočky  a okolního prostředí  a poloměrech křivosti  optických ploch. Platí:

.

Jelikož je nejčastěji čočka obklopena vzduchem o indexu lomu , vztah se v tomto případě zjednoduší:

, kde n je index lomu materiálu čočky.

Při výpočtu ohniskové vzdálenosti je nutné dodržovat znaménkovou konvenci: optické plochy vypuklé (vzhledem k okolnímu prostředí) mají poloměr křivosti kladný a optické plochy duté záporný. Pro ploskovypuklé a ploskoduté čočky se poloměr křivosti , a proto výraz

Charakteristickou veličinou čočky je její optická mohutnost , definovaná jako převrácená hodnota ohniskové vzdálenosti

Jednotkou optické mohutnosti je m^-1. V oční optice se používá vedlejší jednotka optické mohutnosti zvaná dioptrie D. Optickou mohutnost 1 D má čočka s ohniskovou vzdáleností 1 m.

Platí-li pro indexy lomu nerovnost n₂ > n₁ , tj. čočka je opticky hustší než okolní prostředí, pak spojky mají ohniskovou vzdálenost i optickou mohutnost kladnou a pro rozptylky jsou obě veličiny záporné.

• spojky:

• rozptylky:

Pokud by čočka byla umístěna v prostředí o větším indexu lomu, pak by se spojka chovala jako rozptylka a naopak rozptylka jako spojka.

Přílohy