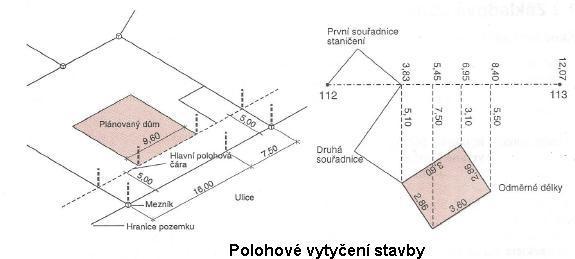
Polohové vytyčení stavby

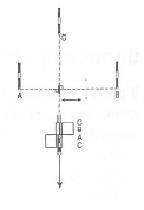
Polohovým vytýčením stavby rozumíme vytýčení rozměrů a tvaru budoucí budovy ve směru vodorovném. Prostorové vytyčení stavby se provádí, jak bylo uvedeno v předešlé kapitole, podle vytyčovacích výkresů v souladu s územním rozhodnutím a stavebním povolením. Vytyčovací výkres obsahuje všechny potřebné údaje pro vytyčení prostorové polohy objektu a jeho rozměru a tvaru. Vytyčení každého objektu se skládá z řady jednoduchých úloh, při kterých se vytyčují body, přímky, úsečky a úhly. Polohu jednotlivých bodů stavebního objektu vytyčujeme různými metodami. Hlavní používaná metoda je metoda polárních pravoúhlých souřadnic.

Obr. 1: Příklad polohového vytyčení stavby

U polohového vytýčení menších staveb lze pravý úhel vytyčit pomocí:

• Vytyčovacího hranolu (dvojitého pentagonu) – při pravém úhlu se v průzoru pentagonu objeví všechny tři výtyčky svisle nad sebou.

          

                                             

   Obr. 2: Schéma vytyčovacího hranolu

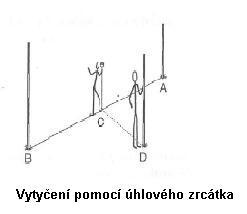
•  Pomocí úhlového zrcátka – skládá se z tělesa s držákem, na kterém je zavěšena olovnice. Olovnice musí přesně směřovat na vytyčovaný bod. Uvnitř tělesa leží proti sobě dvě zrcátka a dvě okénka pod úhlem 45°. Pravý uhel se zaměří pomocí tří výtyček. Pokud dosáhneme krytí zrcadlového obrazu jedné výtyčky s druhou viditelnou v okénku, získali jsme pravý úhel.

                                         

    Obr. 3: Schéma vytyčení pomocí úhlového zrcátka

•   Pomocí pythagorejských čísel – pomocí pásma vytvoříme pravoúhlý trojúhelník s díly 3, 4, 5 (další varianty: 5, 12, 13 nebo 8, 15, 17) nebo jejich násobky.

                                                                                                                                                                           

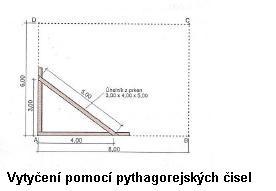
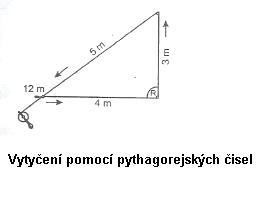
    Obr. 4, 5: Schéma vytyčení pomocí pythagorejských čísel                                             

•   Pomocí rovnoramenného trojúhelníka, který je zhotoven z prken nebo ho lze vytvořit pomocí pásma. Používá se u staveb menších rozměrů např. garáže.

                                                                                                            

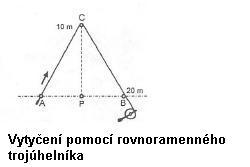
    Obr. 6: Schéma vytyčení pomocí rovnoramenného trojúhelníka    

 

K vytyčení polohopisu stavby potřebujeme:

• teodoli,t
• pásmo, nivelační lať, výtyčky, olovnici, měřičské hřeby, dvojitý pentagon,
• kolíky, kladivo, provaz, stavební dřevo, hřebíky,pila, barva, ochranné tyče atd.,
• v poslední době se k vytyčení využívá totální stanice nebo systém GPS.

Zdroje

• HÁJEK, Václav a kol. Pozemní stavitelství I. Praha: Sobotáles, 2001. ISBN 80-85920-81-6.
• PODLENA, Václav. Zednické práce. Technologie 2. a 3. ročník. Praha: Parta s. r. o., 2003. ISBN 80-7320-018-X.
• TIBITANZL, Otomar., František KODL. Stavební technologie II pro 2. ročník SOU. Praha: SNTL, 1985.

Obrázky:

• Obr. 1, 2, 3, 4, 5, 6 PODLENA, Václav. Zednické práce. Technologie 2. a 3. ročník. Praha: Parta s. r. o., 2003. ISBN 80-7320-018-X.
• Obr. 7: AUTOR NEUVEDEN. Vyměřování v terénu [online]. [cit. 2014-10-28]. Dostupné z: http://www.ekotechnika.cz/dvojity-pentagon-v-kozenem-pouzdru?kat=vymerovani-v-terenu.
• Obr. 8: AUTOR NEUVEDEN. Úhlové zrcátko [online]. [cit. 2014-10-28]. Dostupné z: http://geodezie-duchcov.blog.cz/galerie/pristroje-konce-19-stoleti-a-20-stoleti-popis/obrazek/27173298.
• Obr. 9: AUTOR NEUVEDEN. [online]. [cit. 2014-10-28]. Dostupné z: http://cs.wikipedia.org/wiki/Pythagoras.