Elektronická učebnice

Přenos výkonu ze zdroje do zátěže

Přenos činného výkonu ze zdroje s napětím U₀ a vnitřním odporem R_i do zátěže s odporem R_z v obvodu podle obr. 3 z předchozí kapitoly je možné určit ze vztahu

$P_{R_{z}}= R_{z}\cdot I^{2}$

Proud, který prochází obvodem, se vypočítá z Ohmova zákona

$I= \frac{U_{0}}{R_{i}+R_{z}}$

Dosazením do předcházejícího vztahu dostaneme

$P_{R_{z}}= R_{z}\left ( \frac{U_{0}}{\left ( R_{i}+R_{z} \right )} \right )^{2}$

Po drobné úpravě

$P_{R_{z}}= U_{0}^{2}\frac{R_{z}}{\left ( R_{i}+R_{z} \right )^{2}}$

Po zkrácení předcházejícího vztahu druhou mocninou vnitřního odporu obdržíme vztah

$P_{R_{z}}= U_{0}^{2}\frac{\frac{R_{z}}{R_{i}^{2}}}{\frac{\left ( R_{i}+R_{z} \right )^{2}}{R_{i}^{2}}}= U_{0}\frac{U_{0}}{R_{i}}\frac{\frac{R_{z}}{R_{i}}}{\left ( \frac{R_{i}+R_{z}}{R_{i}} \right )^{2}}= U_{0}I_{k}\frac{\frac{R_{z}}{R_{i}}}{\left ( 1+\frac{R_{z}}{R^{_{i}}} \right )^{2}}$

Výsledný vztah

$P_{R_{z}}=U_{0}I_{k}\frac{\frac{R_{z}}{R_{i}}}{\left ( 1+\frac{R_{z}}{R_{i}} \right )^{2}}$

Z tohoto vztahu je patrné, že výkon na zátěži závisí na poměru odporu zátěže a vnitřního odporu zdroje. Součin charakteristických veličin (U₀, I_k) je roven maximální hodnotě tzv. celkového výkonu zdroje při zkratovaných výstupních svorkách (R_z = 0). Výstupní napětí je nulové a veškerý výkon se spotřebovává na vnitřním odporu zdroje v teplo.

$P_{c max}= U_{0}I_{k}$

$P_{R_{z}}= P_{c max}\frac{\frac{R_{z}}{R_{i}}}{\left ( 1+\frac{R_{z}}{R_{i}} \right )^{2}}$

Možné stavy pro výkon na zátěži při různých hodnotách R_z:

a) R_z = 0 => P_Rz = 0 R_z = 0 výstupní svorky jsou zkratované;

b) R_z = R_i => P_Rz = U₀ I_k /4 největší výkon dosažitelný na zátěži, je to však jen čtvrtina P_cmax;

c) R_z → ∞ => P_Rz = 0 R_z → ∞ výstupní svorky jsou rozpojené.

Poznámka:

Pro stanovení závěru podle bodu c není správné dosadit do výsledného vztahu nekonečně velikou hodnotu příslušné veličiny v tomto případě R_z, ale je nutná úprava vztahu pro výkon na zátěži, protože matematické operace s veličinami, jejichž hodnoty rostou nade všechny meze (nekonečno), vyžadují napřed korektní matematické úpravy odvozených vztahů obecně tak, aby dosazení nekonečně velké hodnoty vedlo ke zcela jednoznačným závěrům. Pro další řešení je nejlépe zavést substituci R_z/R_i = x a pak krátit zlomek x².

$P_{R_{z}}= U_{0}I_{k}\frac{\frac{R_{z}}{R_{i}}}{\left ( 1+\frac{R_{z}}{R_{i}} \right )^{2}}= U_{0}I_{k}\frac{x}{\left ( 1+x \right )^{2}}= U_{0}I_{k}\frac{\frac{1}{x}}{\left ( \frac{1}{x}+1 \right )^{2}}$

Do takto upraveného vztahu lze dosadit x→ ∞, což je stejné jako když R_z→ ∞. Zlomek 1/x zcela jednoznačně míří k 0 a výkon na zátěži rovněž (P_Rz = 0).

Celkový výkon zdroje je dán součtem výkonu na vnitřním odporu zdroje a výkonem na zatěžovacím odporu.

$P_{c}= P_{R_{i}}+P_{R_{z}}$

Po dosazení dílčích vztahů a úpravách získáme vztah

$P_{c}= U_{0}I_{k}\frac{1}{1+\frac{R_{z}}{R_{i}}}$

Je možné ho také vypočítat ze vztahu

$P_{c}= \left ( \frac{U_{0}}{R_{i}+R_{z}} \right )^{2}$

Po příslušných úpravách

$P_{c}= U_{0}I_{k}\frac{1}{1+\frac{R_{z}}{R_{i}}}$

Možné stavy celkového výkonu zdroje pro specifické hodnoty R_z:

a) R_z = 0 => P_c = U₀ I_k R_z = 0 výstupní svorky jsou zkratované, veškerý výkon se spotřebovává na vnitřním odporu zdroje, je to maximální hodnota celkového výkonu, P_c = P_cmax;

b) R_z = R_i => P_c = U₀ I_k /2 polovina maximální hodnoty celkového výkonu, čtvrtina se spotřebovává na zátěži a čtvrtina na vnitřním odporu zdroje;

c) R_z → ∞ => P_c = 0 R_z → ∞ výstupní svorky jsou rozpojené.

Z předcházejících vztahů pro pro oba výkony lze nakreslit jejich závislosti na poměru R_z/R_i (obr. 1).

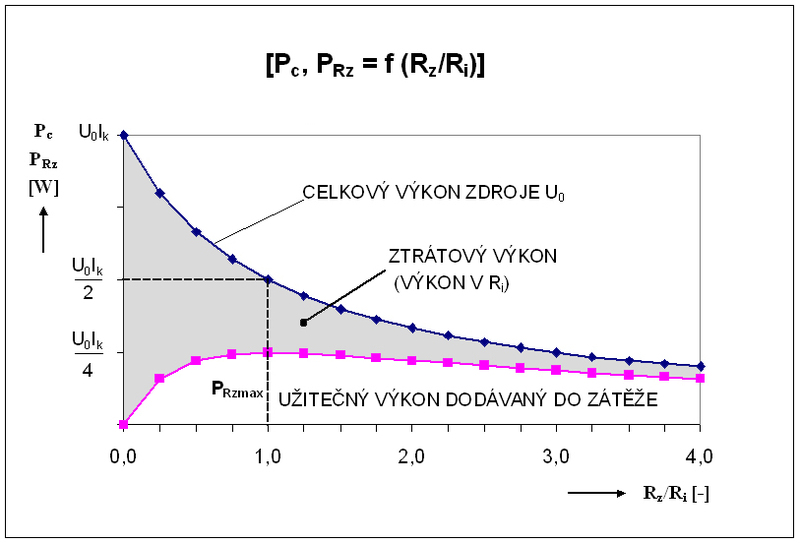
Obr. 1: Závislost celkového výkonu a výkonu na zátěži na poměru odporu zátěže a vnitřního odporu zdroje

Zdroje

KOUTNÝ, Jaroslav a Ivo VLK. Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009

Obrázky

Obr. 1: KOUTNÝ, Jaroslav a Ivo VLK. Závislost celkového výkonu a výkonu na zátěži na poměru odporu zátěže a vnitřního odporu zdroje, Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009

Metodika práce se systémem ELUC
Nastavení Cookies