Elektronická učebnice

Théveninova věta

Jakýkoliv aktivní lineární jednobran (tj. obvod složený z lineárních pasivních součástek a z lineárních zdrojů) je možné nahradit sériovým zapojením ideálního zdroje napětí U₀ a odporu R_i, přičemž U₀ je napětí naprázdno na svorkách původního jednobranu a R_i je jeho odpor.

Při výpočtu náhradního vnitřního odporu R_i se nahradí všechny zdroje elektrické energie obsažené ve zjednodušované části obvodu jejich vlastními vnitřními odpory, což znamená, že všechny ideální zdroje napětí se nahradí zkratem a ideální zdroje proudu se nahradí rozpojenými svorkami.

Použití Théveninovy věty je nejlepší ukázat na jednoduchém obvodu (obr. 1) a jeho náhradním zapojení (obr. 2):

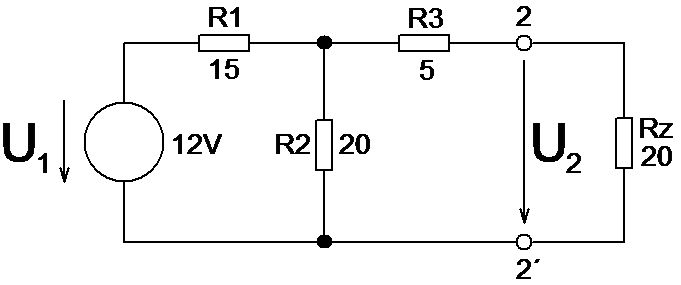
Obr. 1: Zapojení obvodu pro řešení pomocí Théveninovy věty

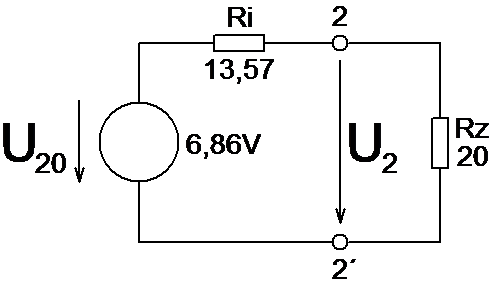
Obr. 2: Zapojení náhradního obvodu podle Théveninovy věty

Stanovení napětí naprázdno na výstupních svorkách 2 – 2´ (zátěž R_z je odpojena, obr. 3).

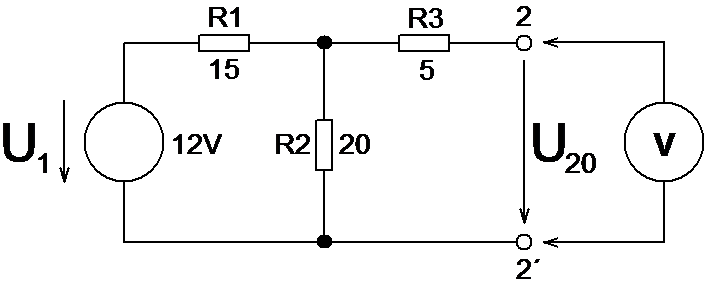
Obr. 3: Zapojení pro stanovení napětí naprázdno podle Théveninovy věty

$U_{20}= R_{2}\frac{U_{1}}{R_{1}+R_{2}}$

Po dosazení

$U_{20}= 20\frac{12}{15+20}= 6,86V$

Výpočet vnitřního odporu náhradního obvodu (ideální zdroj napětí U₁ se na nahradí zkratem, obr. 4).

Obr. 4: Zapojení pro stanovení vnitřního odporu podle Théveninovy věty

$R_{i}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}+R_{3}$

Po dosazení

$R_{i}\frac{15\cdot 20}{15+20}+5= 13,57\Omega$

Parametry náhradního obvodu a jeho zapojení (obr. 5).

$U_{20}= 6,86V$ $R_{i}= 13,57\Omega$

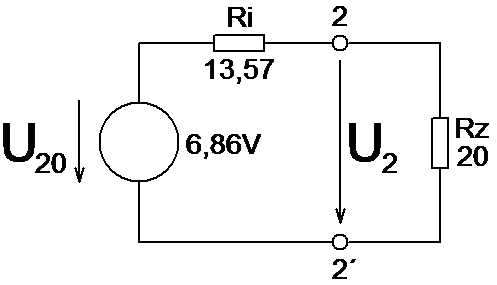
Obr. 5: Zapojení náhradního obvodu podle Théveninovy věty s vypočítanými hodnotami

Théveninova věta se dále používá při řešení zatížených odporových děličů napětí, kdy úkolem je stanovit hodnoty odporů děliče tak, aby dělič měl minimální vlastní spotřebu (tzn., že dělič se skládá z rezistorů s co největší odporovou hodnotou, ale přitom změna výstupního napětí je v souladu se změnou zatěžovacího proudu).

Příklad

Navrhněte odporový dělič s minimální vlastní spotřebou, na jehož výstupu bude při odběru proudu I₂ = 100 mA napětí U₂ = 12 V. Zvýší-li se odběr proudu na dvojnásobek, smí výstupní napětí klesnout nejvýše na 10 V. Vstupní napětí U₁ = 35 V. Vypočítejte také proud procházející děličem naprázdno I₀ (obr. 6).

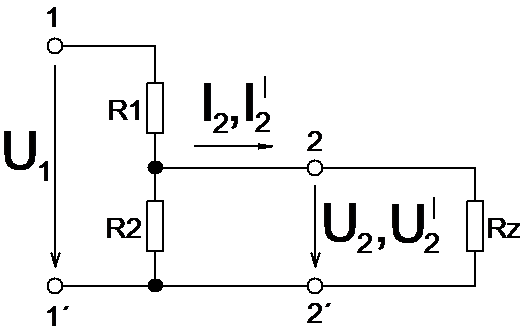
Obr. 6: Zapojení zatíženého děliče napětí

Stanovení vnitřního odporu náhradního obvodu (podle Théveninovy věty)

$R_{i}\frac{R_{1}R_{2}}{R_{1}+R_{2}}= -\frac{\Delta U_{2}}{\Delta I_{2}}= -\frac{U_{2}-U_{2}^{'}}{I_{2}-I_{2}^{'}}$

$I_{2}^{'}= 2I_{2}= 2\cdot 100= 200 mA = 0.2 A$

$\Delta U_{2}= U_{2}-U_{2}^{'}= 12-10= 2 V$

$\Delta I_{2}= I_{2}-I_{2}^{'}= 0,1-0,2= -0,1 A$

$R_{i}= \frac{R_{1}R_{2}}{R_{1}+R_{2}}= -\frac{\Delta U_{2}}{\Delta I_{2}}=-\frac{2}{0,1}=20 \Omega$

Výstupní napětí naprázdno je možné stanovit ze vztahu

$U_{2}= U_{20}-R_{i}I_{2}\Rightarrow U_{20}=U_{2}+R_{i}I_{2}$

$U_{20}=12+20\cdot 0,1=14 V$

Ze vztahu pro vnitřní odpor také vyplývá

$R_{i}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}\Rightarrow \frac{R_{i}}{R_{1}}=\frac{R_{2}}{R_{1}+R_{2}}$

Výstupní napětí děliče naprázdno (bez zatížení)

$U_{20}=R_{2}\frac{U_{1}}{R_{1}+R_{2}}\Rightarrow \frac{U_{20}}{U_{1}}=\frac{R_{2}}{R_{1}+R_{2}}$

Porovnáním dvou přecházejících vztahů se získá rovnice

$\frac{U_{20}}{U_{1}}=\frac{R_{i}}{R_{1}}\Rightarrow R_{1}=R_{i}\frac{U_{1}}{U_{20}}=20\frac{35}{14}=50 \Omega$

Druhý odpor děliče se určí ze vztahu pro vnitřní odpor

$R_{i}=\frac{R_{1}R_{2}}{R_{1}+R_{2}}\Rightarrow R_{2}=\frac{R_{i}R_{1}}{R_{1}-R_{i}}=\frac{20\cdot 50}{50-20}=33,33 \Omega$

Proud procházející děličem naprázdno

$I_{0}=\frac{U_{1}}{R_{1}+R_{2}}=\frac{35}{50+33,33}=0,42 A$

Kontrola – výpočet napětí naprázdno

$U_{20}=R_{2}\frac{U_{1}}{R_{1}+R_{2}}=33,33\frac{35}{50+33,33}=14 V$

Zdroje

KOUTNÝ, Jaroslav a Ivo VLK. Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009

Obrázky

Obr. 1: KOUTNÝ, Jaroslav a Ivo VLK. Zapojení obvodu pro řešení pomocí Théveninovy věty, Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009
Obr. 2: KOUTNÝ, Jaroslav a Ivo VLK. Zapojení náhradního obvodu podle Théveninovy věty, Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009
Obr. 3: KOUTNÝ, Jaroslav a Ivo VLK. Zapojení pro stanovení napětí naprázdno podle Théveninovy věty, Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009
Obr. 4: KOUTNÝ, Jaroslav a Ivo VLK. Zapojení pro stanovení vnitřního odporu podle Théveninovy věty, Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009
Obr. 5: KOUTNÝ, Jaroslav a Ivo VLK. Zapojení náhradního obvodu podle Théveninovy věty s vypočítanými hodnotami, Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009
Obr. 6: KOUTNÝ, Jaroslav a Ivo VLK. Zapojení zatíženého děliče napětí, Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009

Metodika práce se systémem ELUC
Nastavení Cookies