Základní parametry bipolárních tranzistorů

Čtyřpólové parametry tranzistoru pro malé signály

Nejjednodušší model tranzistoru je dán vztahem i_C = β . i_B, podrobnější model je popsán rovnicí

I_C = f(i_B; u_CE)

Vlastnosti obecného lineárního dvojbranu je možné popsat dvojicí charakteristických vlastností, které vyjadřují vzájemné vztahy mezi vstupními a výstupními veličinami. První z rovnic se vztahuje ke vstupu dvojbranu, druhá rovnice se vztahuje k výstupu dvojhranu. Vstup a výstup je nahrazován zapojením podle Théveninova nebo Nortonova teorému.

Hodnota parametrů tranzistoru závisí na:

základním zapojení: SB, SE, SC;
poloze klidového pracovního bodu;
kmitočtu přenášeného signálu;
teplotě tranzistoru – běžně jsou měřeny při teplotě ϑ= 25 ℃.

Model bipolárního tranzistoru pomocí hybridních parametrů

Pro popis bipolárního tranzistoru jsou v oblasti nízkých kmitočtů nejčastěji používány tzv. hybridní parametry. Při jejich použití je vstup tranzistoru modelován zapojením pomocí Théveninovy poučky a výstup pomocí Nortonovy poučky.

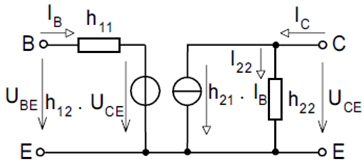
Obr. 1: Model bipolárního tranzistoru pomocí h-parametrů

Proto vyjádříme vstupní rovnici jakou součet napětí, výstupní jako součet proudů:

U_BE = h₁₁. I_B + h₁₂ . U_CE

I_C = h₂₁ . I_B + h₂₂ . U_CE

Jak již víme, může být tranzistor zapojen se společnou bází, se společným kolektorem a se společným emitorem. Pro zapojení se společným kolektorem a se společným emitorem používáme stejné parametry – parametry odvozené pro zapojení se společným emitorem.

Výrobci tranzistorů měří dva typy parametrů:

stejnosměrné;
střídavé (nízkofrekvenční, vysokofrekvenční).

Index _E u parametrů je používán u zapojení tranzistoru se společným emitorem;

Index _B u parametrů zapojení tranzistoru se společnou bází.

Abychom rozlišili, zda se jedná o stejnosměrné či střídavé parametry, budeme v dalším textu používat písmena malé abecedy pro index střídavých parametrů (např. h_21e), pro index stejnosměrných parametrů písmena velké abecedy (např. h_21E). Stejnosměrné parametry popisují vlastnosti tranzistoru v určitém pracovním bodu , není-li přiváděn signál, vyjadřují závislosti stejnosměrných (napájecích) proudů a napětí tranzistoru.

Střídavé parametry (dynamické) se vztahují ke střídavému signálu přivedenému na vstup daného zapojení tranzistoru. Přivedený signál má tak malou úroveň, aby jeho další zmenšování již nemělo vliv na velikost naměřeného parametru. Hodnoty, uvedené v katalozích firem, jsou vztaženy k určitému kmitočtu, např. 1 kHz.

Ve vztazích pro určení jednotlivých parametrů jsou velkými písmeny U a I označována stejnosměrná napětí a proudy, výrazy Δu a Δi označují velikosti napětí a proudů signálu.

Model tranzistoru pomocí hybridních parametrů

Definice h₁₁

Střídavý parametr - označme velikosti střídavého napětí a proudu vstupního signálu Δu₁ a Δi₁, potom:

$h_{11}=\frac{\Delta u_{1}}{\Delta i_{1}}$ ( U₂ = konst., Δu₂ = 0) vstupní odpor, zátěž nakrátko

Stejnosměrný parametr - označme velikost vstupního stejnosměrného proudu I₁ a napětí U₁, potom:

$h_{11}=\frac{u_{1}}{i_{1}}$ (U₂ = 0 [Ω]) vstupní odpor, výstup nakrátko

Definice h₁₂

Střídavý parametr $h_{21}=\frac{\Delta u_{1}}{\Delta u_{2}}$ ( I₁ = konst.) zpětný napěťový činitel

Stejnosměrný parametr $h_{12}=\frac{u_{1}}{u_{2}}$ (I₁ = 0) stejnosměrný zpětný napěťový činitel

Tento parametr charakterizuje velikost zpětného ovlivňování vstupu tranzistoru velikostí výstupního napětí.

Definice h₂₁

Je to nejdůležitější parametr tranzistoru, má význam proudového zesilovacího činitele:

Střídavý parametr:

$h_{21}=\frac{\Delta i_{2}}{\Delta i_{1}}$ ( U₁ = konst., Δu₂ = 0 ) proudový zesilovací činitel, zátěž nakrátko

Stejnosměrný parametr $h_{21}=\frac{i_{2}}{i_{1}}$ (U₂ = 0) proudový zesilovací činitel nakrátko

Definice h₂₂

Střídavý parametr $h_{22}=\frac{\Delta i_{2}}{\Delta u_{2}}$ ( I₁ = konst., Δi₁ = 0 ) 〔S〕 výstupní vodivost

Stejnosměrný parametr $h_{22}=\frac{I_{2}}{U_{2}}$ (I₁ = 0) 〔S〕 výstupní vodivost naprázdno

Obecně jsou h parametry tranzistoru komplexní veličiny obsahující rezistory a kondenzátory. Vlivem parazitních kapacit je omezen rozsah kmitočtů, ve kterých je tranzistor aktivním prvkem (každý PN přechod je zároveň kondenzátorem).

Model tranzistoru pomocí admitančních parametrů

Kromě hybridních parametrů je model tranzistoru znázorňován též pomocí admitančních parametrů. Při jejich použití je vstup i výstup tranzistoru modelován pomocí Nortonovy poučky. Model tranzistoru v zapojení SE je znázorněn na obrázku 2.

Proto vyjádříme vstupní i výstupní parametry v zapojení SE jako součet proudů:

I_B = y₁₁ . U_BE + y₁₂ . U_CE

Ic = y₂₁ . U_BE + y₂₂ . U_CE, v maticovém tvaru

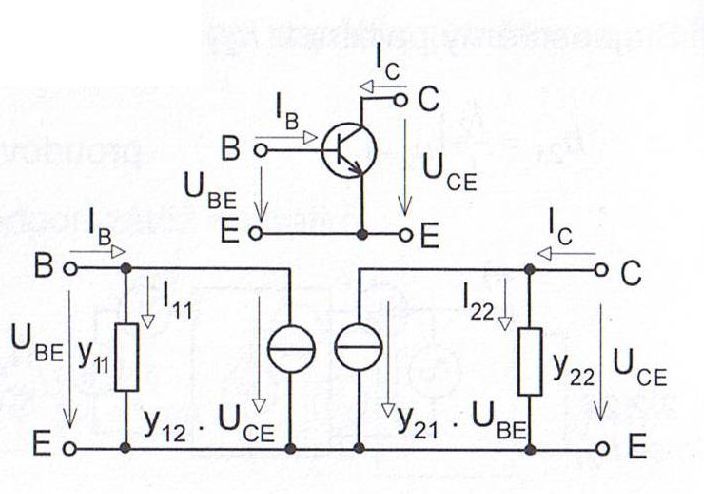
Obr. 2: Model tranzistrou pomocí admitančních parametrů

Dále budeme definovat pouze střídavé parametry

$y_{11e}=\frac{\Delta i_{B}}{\Delta u_{BE}}$ (U_CE = konst., Δu_CE=0) vstupní vodivost tranzistoru, zátěž je zkratována

$y_{12e}=\frac{\Delta i_{B}}{\Delta u_{CE}}$ (U_BE = konst., Δu_BE=0) zpětná vodivost, zdroj signálu zkratován

$y_{21}=\frac{\Delta i_{C}}{\Delta u_{BE}}$ (U_CE = konst., Δu_CE=0) přenosová vodivost, zátěž kratována (to je údaj, který

říká, jak se změní kolektorový proud, když změníme

napětí mezi bází a emitorem, což je strmost převodní

charakteristiky tranzistoru)

$y_{22}=\frac{\Delta i_{C}}{\Delta u_{CE}}$ (U_B1 = konst., Δu_BE=0) výstupní vodivost tranzistoru, zdroj signálu je

zkratován

Přepočet hybridních parametrů na admitanční a naopak se řídí následujícími vztahy:

$y_{11}=\frac{1}{h_{11}}$ $h_{11}=\frac{1}{y_{11}}$

$y_{12}=\frac{-h_{12}}{h_{11}}$ $h_{12}=\frac{y_{12}}{y_{11}}$

$y_{21}=\frac{h_{21}}{h_{11}}$ $h_{21}=\frac{y_{21}}{y_{11}}$ D_y = y₁₁ . y₂₂ – y₁₂ . y₂₁

$y_{22}=\frac{D_{h}}{h_{11}}$ $h_{22}=\frac{D_{y}}{y_{11}}$ D_h = h₁₁ . h₂₂ – h₁₂ . h₂₁

Teplotní závislost parametrů bipolárních tranzistorů

Vzhledem ke značné teplotní závislosti tranzistorů je nutné je pokládat také za prvky řízené teplotou. Vliv teploty na průběh jejich charakteristik a změny parametrů je poměrně velký. Z hlediska použití tranzistorů nás nejvíce zajímají teplotní změny kolektorového proudu.

Vliv teploty na kolektorový proud I_c křemíkových tranzistorů

Změna kolektorového proudu je výsledným produktem teplotní závislosti hlavně těchto veličin:

zbytkového proudu kolektor-báze I_CB0 a tedy i I_CE0. Zbytkový proud se při změně teploty o 10 ℃ přibližně zdvojnásobí. To se projeví na změně velikosti kolektorového proudu;
stejnosměrného proudového zesilovacího činitele h_21E;
napětí báze-emitor U_BE potřebného pro nastavení proudu kolektoru → při konstantním proudu emitoru a nepříliš velkých změnách teploty se napětí na emitorovém přechodu mění o -(2 až 3) mV/℃.

Pro křemíkové tranzistory je rozhodující teplotní změna napětí na přechodu báze-emitor (U_BE). Zbytkové proudy jsou řádově nA a většinou se jejich vliv téměř neuplatní.

Nejhůře z běžných polovodivých materiálů je na tom germanium. Teplotní závislost je u germaniových tranzistorů tak velká, že může zbytkový proud I_CE0 dosáhnout při vyšších teplotách velikosti řádově μA a jeho vliv může začít převažovat. Zatímco u křemíkových tranzistorů vliv I_CE0 většinou zanedbáváme, u germaniových tranzistorů I_CE0zanedbat nelze.

Teplota přechodů tranzistoru je ovlivňována:

teplotou prostředí;
kolektorovou ztrátou;
účinností chlazení tranzistoru.

Kolektorová ztráta P_c:

Při provozu tranzistoru protéká emitorovým i kolektorovým přechodem přibližně stejný proud

(I_E = I_C + I_B ≅ I_C)

Na závěrně polarizovaném kolektorovém přechodu je mnohem větší úbytek napětí než na propustně polarizovaném emitorovém přechodu. Proto je při stejné velikosti protékajícího proudu vznik tepla na kolektorovém přechodu mnohem větší.

K celkovému oteplení tranzistoru tedy přispívá rozhodující měrou vývin tepla na kolektoru. Jeho velikost udává tzv. kolektorová ztráta, která má označení P_c. Hodnotu kolektorové ztráty určíme součinem

P_c = U_CE . I_C

P_Cmax je mezní přípustný ztrátový výkon tranzistoru při referenční teplotě pouzdra.

Teplotní odolnost tranzistoru můžeme zlepšit pomocí účinného chlazení.

Je-li tranzistor opatřen chladičem, je odpovídajícím způsobem zvýšena jeho přípustná kolektorová ztráta. Účinnost chlazení závisí na:

způsobu upevnění tranzistoru k chladiči;
na přítlačné síle, kterou je tranzistor přitlačen k chladiči;
na opracování povrchů chladiče a tranzistoru, na rovinnosti dosedajících ploch;
na použitých prostředcích pro zlepšení teplotního styku mezi tranzistorem a chladičem (např. silikonová vazelína apod.);
na umístění chlazeného tranzistoru v zařízení (zda je umístěn v místě, kde dochází k hromadění tepla, nebo kde naopak je chladný vzduch, případně zda neofukujeme chladič tranzistoru nuceně ventilátorem apod.).

Všechny výše uvedené závislosti mají vliv na stabilitu nastavení pracovního bodu. K nim je nutné připočítat změny vlivem stárnutí, rozptylu parametrů tranzistorů, změny napájecího napětí apod.

Důležité mezní parametry bipolárních tranzistorů

Mezní parametry tranzistorů patří mezi nejdůležitější údaj uváděné výrobcem tranzistoru, protože na jejich respektování závisí spolehlivost zařízení, ve kterém tranzistory pracují.

Pracovní oblast tranzistorů je omezena mezními parametry, při jejichž překročení hrozí nebezpečí zničení tranzistoru. K těmto parametrům patří zejména:

maximální kolektorová ztráta P_Cmax - je určena nejvyšší povolenou teplotou kolektorového přechodu. Oblast, ve které je překročena maximální povolená kolektorová ztráta, je dána hyperbolou dle vztahu

P_{Z =}U_BE . I_B + U_CB . I_C ≅ U_CE . I_C = P_C

maximální kolektorový proud I_Cmax - je určen konstrukcí tranzistoru. Podobně jako při překročení maximální kolektorové ztráty, může dojít při překročení I_Cmax k přehřátí kolektorového přechodu tranzistoru;
mezní napětí kolektor-emitor U_CEmax - je napětí mezi kolektorem a emitorem při rozpojeném obvodu báze. Při překročení tohoto mezního napětí může dojít k napěťovému průrazu a ke zničení přechodu kolektor-báze. Je-li kolektorový proud omezen odporem dostatečné velikosti, je tento průraz nedestruktivní - používá se pro jeho měření.
maximální proud báze I_Bmax - jeho velikost je určena konstrukcí tranzistoru, u výkonových tranzistorů je větší než u tranzistorů malého výkonu;
mezní napětí emitor-báze U_EB0 - je to mezní napětí závěrně polarizovaného přechodu mezi emitorem a bází. Toto mezní napětí má velikost řádově jednotky voltů (např.5V). Je-li závěrný proud báze omezen odporem dostatečné velikosti, je průraz závěrně polarizovaného přechodu emitor-báze nedestruktivní.

Zdroje

KOUTNÝ, Jaroslav a Ivo VLK. Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009

Obrázky

Obr. 1: KOUTNÝ, Jaroslav a Ivo VLK. Model bipolárního tranzistoru pomocí h-parametrů, Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009
Obr. 2: KOUTNÝ, Jaroslav a Ivo VLK. Model tranzistrou pomocí admitančních parametrů, Elektronika I učebnice. VYTVOŘENO V RÁMCI PROJEKTU: DIGITÁLNÍ ŠKOLA: ICT VE VÝUCE TECHNICKÝCH PŘEDMĚTŮ, REG. Č. CZ.1.07/1.1.04/01.0137, Vyšší odborná škola a Střední průmyslová škola elektrotechnická, Olomouc 2009