Elektronická učebnice

Přechodová charakteristika integračního a derivačního dvojbranu

Definice

Derivační článek (derivátor) je elektrotechnický obvod, který provádí matematickou funkci derivování – napětí na výstupu je derivací napětí na vstupu podle času.

Integrační článek (integrátor) je elektrotechnický obvod, který provádí matematickou funkci integrování – napětí na výstupu je integrálem napětí na vstupu podle času.

obrazek

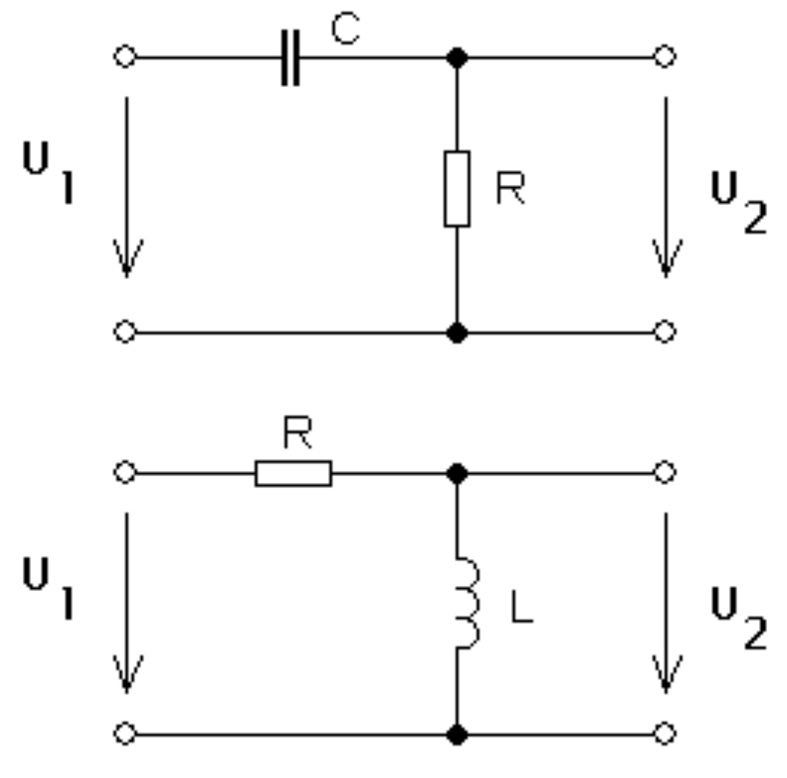
Obr. 1: Derivační článek

obrazek

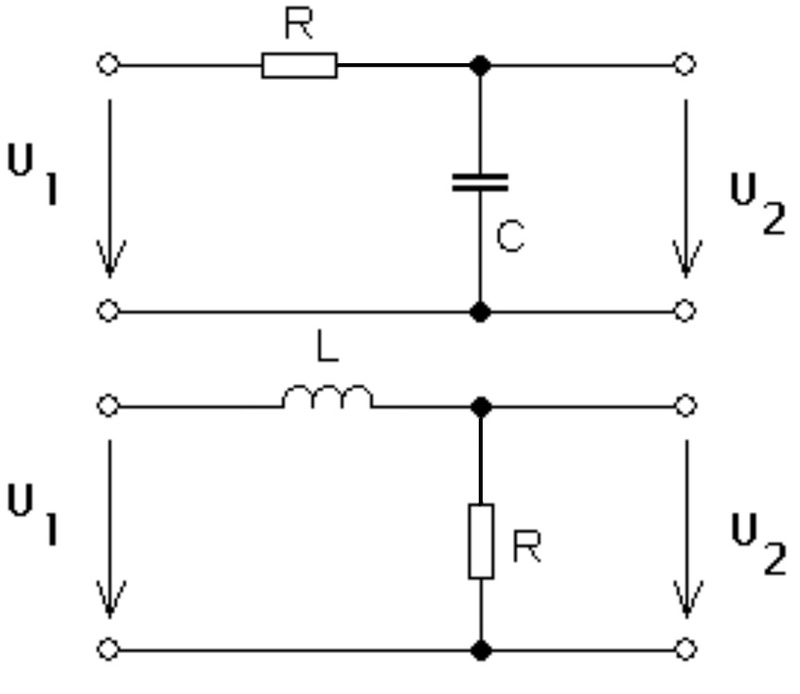
Obr. 2: Integrační článek

Derivační a integrační článek obsahuje nejméně jednu kmitočtově závislou součástku (kondenzátor, cívka). Nejjednodušším zapojením je pasivní zapojení využívající jeden kondenzátor, či cívku. Aktivní elektronický derivátor i integrátor obsahuje operační zesilovač s rezistorem a kondenzátorem. Derivační článek má frekvenční charakteristiku horní propusti – se zvyšující se frekvencí vstupního napětí výstupní napětí roste, integrační článek má naopak frekvenční charakteristiku dolní propusti – se zvyšující se frekvencí vstupního napětí výstupní napětí klesá. V odborné literatuře jsou tyto obvodové prvky označovány také jako články, čtyřpóly, dvojbrany či filtry.

Napěťový přenos

Napěťový přenos A je důležitou charakteristickou veličinou těchto obvodů. Je definován vztahem: A = U₂/ U₁.
U₁ je vstupní a U₂ výstupní napětí členu.

Pro integrační článek platí:

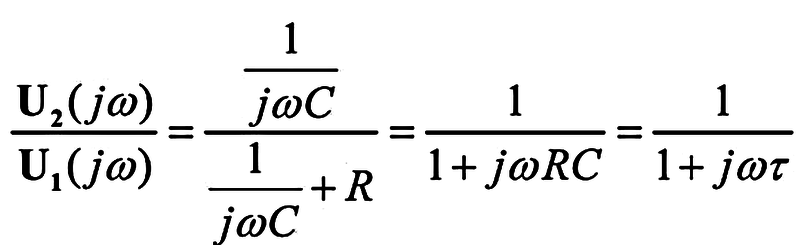
Přenosová charakteristika

Grafická závislost absolutní hodnoty přenosu napětí na frekvenci se nazývá přenosová charakteristika. Přenos se vyjadřuje obvykle v decibelech:

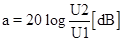Přenos napětí pro integrační člen RC lze vypočítat ze vztahu:

kde ω je kruhová frekvence střídavého proudu, C je kapacita kondenzátoru a R ohmický odpor rezistoru. Pokud je ω.C.R « 1, je napěťový přenos přibližně roven jedné. Jestliže ω.C.R = 1, pak pro poměr napětí platí:

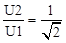V tomto případě činí útlum -3dB. Tomuto poměru napětí odpovídá kmitočet, který se nazývá mezní (kritický) a lze jej vyjádřit vztahem:

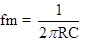Po dosazení do vztahu pro A můžeme výraz upravit do podoby:

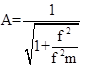kde f je libovolná frekvence střídavého proudu. Pokud je ω.C.R»1, neboli f > f_m, je přenos napětí výrazně menší než jedna. Tohoto jevu se používá k filtraci. Integrační člen RC působí jako dolní propust (horní zádrž). Od mezního kmitočtu jsou vyšší frekvence postupně stále více omezovány.

Derivační článek:

U derivačního členu RC je tomu naopak. Absolutní hodnotu přenosu lze vyjádřit vztahem:

Dosažené frekvence jsou v obráceném poměru. Napěťový přenos menší než jedna nastává pro f < f_m. Derivační člen proto působí jako horní propust (dolní zádrž). Od mezního kmitočtu jsou nižší frekvence stále více potlačovány.

Výše uvedený popis platí pro ideální impedanční přizpůsobení vstupů i výstupů těchto členů. Zdroj signálu má nulový vnitřní odpor, výstup článku je nezatížen. Názvy článků jsou odvozeny od jejich chování při aplikaci obdélníkových napěťových pulzů.

Přechodové charakteristiky integračního a derivačního článku

obrazek

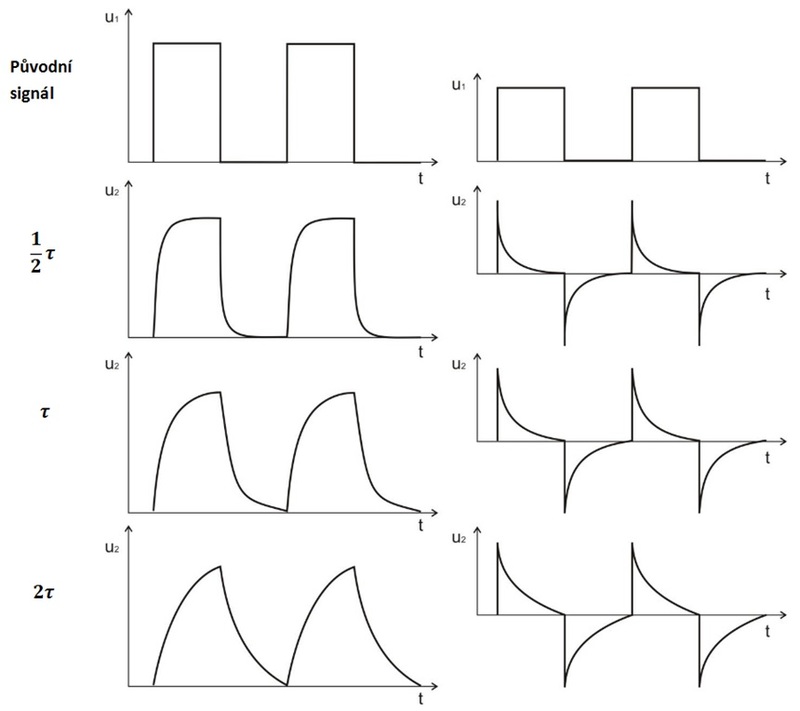
Obr. 3: Přechodové charakteristiky integračního a derivačního článku

Na obr. 3 jsou uvedeny časové průběhy napětí na vstupu a výstupu integračního (vlevo) a derivačního článku pro různé časové konstanty obou článků.

V prvním případě byla nastavena časová konstanta článku na hodnotu 1/2 τ, potom τ a nakonec 2 τ. Vhodné je měnit časovou konstantu velikostí odporu rezistoru v článku. τ=RC nebo τ=L/R. Při větší hodnotě odporu se kondenzátor nabíjí pomaleji.

Komplexní přenos

Komplexní přenos derivačního článku se dá vyjádřit vztahem:

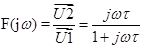kde τ = RC pro obvod s rezistorem, pro obvod s cívkou platí τ = L/R. F je komplexní číslo a má stejný význam jako A.

Na derivačním článku dochází k fázovému posunutí mezi vstupním a výstupním signálem, které je závislé na frekvenci signálu: s rostoucí frekvencí se posuv snižuje, asymptoticky dosahuje pro vysoké frekvence 0°. U frekvence, při které dochází k poklesu napětí −3 dB (A_U = 0,707), je fázový posuv roven 45°. Komplexní přenos se dá vyjádřit jako amplitudová-fázová frekvenční charakteristika v komplexní rovině, nebo se rozdělí na dvě samostatné charakteristiky, útlumovou a fázovou.

Logaritmická amplitudová frekvenční charakteristika derivačního článku

Logaritmická amplitudová frekvenční charakteristika (LAFCH) derivačního článku s rezistorem a kondenzátorem se dá vyjádřit vztahem:.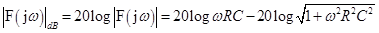

První člen LAFCH tvoří přímku stoupající se strmostí 20dB/dek, která protíná osu x v bodě ω₀ = 1/RC (na obr. černě). Je-li ωRC»1, můžeme jedničku v odmocnině zanedbat, a dostáváme tak přímku s počátkem ve zlomovém kmitočtu ω₀, která klesá se strmostí -20dB/dek.

Logaritmická amplitudová frekvenční charakteristika (LAFCH) derivačního článku s rezistorem a cívkou se dá vyjádřit vztahem:.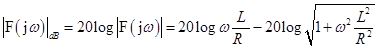

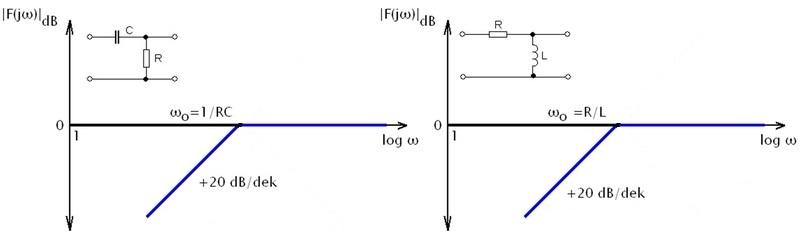
Obr. 4: LAFCH derivačního článku

Komplexní přenos integračního článku

Komplexní přenos integračního článku se vypočítá podle vztahu:

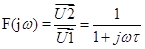kde τ = RC pro rezistor, pro cívku τ = L/R.

Na integrátoru dochází k fázovému posunutí mezi vstupním a výstupním signálem, které je opět závislé na frekvenci signálu: s rostoucí frekvencí se posuv zvyšuje, asymptoticky dosahuje pro vysoké frekvence -90°. U frekvence, při které dochází k poklesu napětí −3 dB (AU = 0,707), je fázový posuv roven -45°. Komplexní přenos je fázor. Dá se vyjádřit jako amplitudová-fázová frekvenční charakteristika v komplexní rovině, nebo se rozdělí na dvě samostatné charakteristiky, útlumovou a fázovou.

Logaritmická amplitudová frekvenční charakteristika integračního článku

Logaritmická amplitudová frekvenční charakteristika (LAFCH) integračního článku s rezistorem a kondenzátorem se dá vyjádřit vztahem:

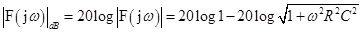První člen LAFCH je roven nule. Je-li ωCR»1, můžeme jedničku v odmocnině zanedbat, a dostáváme tak přímku s počátkem ve zlomové úhlové frekvenci ω0 která klesá se strmostí -20 dB/dek.

Logaritmická amplitudová frekvenční charakteristika (LAFCH) integračního článku s rezistorem a cívkou je:

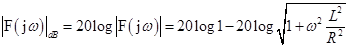První člen LAFCH je roven nule. Je-li ωL/R»1, můžeme jedničku v odmocnině zanedbat a dostáváme tak přímku s počátkem ve zlomové úhlové frekvenci ω₀ která klesá se strmostí -20 dB/dek.

obrazek

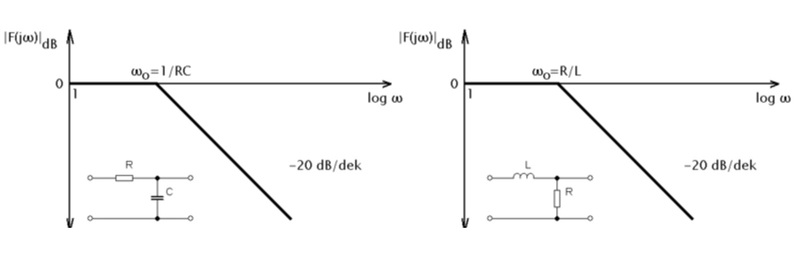
Obr. 5: LAFCH integračního článku

Fázová frekvenční charakteristika

Fázová frekvenční charakteristika se dá vyjádřit vztahem:

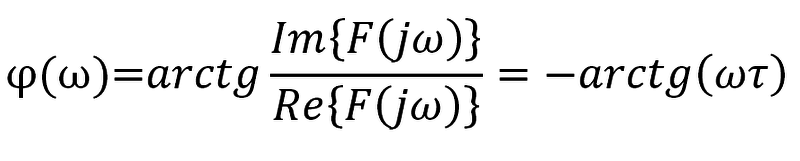Pro RC článek φ(ω) = - arctg(ωRC),

pro RL článek:

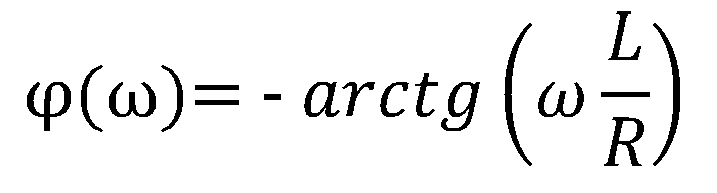
Každému zlomu logaritmické amplitudové frekvenční charakteristiky o -20 dB/dek (resp. + 20 dB/dek) odpovídá posun fáze o -90° (resp. +90°).

Zdroje

BRINDL, Pavel. VY_32_inovace_03_ELE_3_ Elektronické obvody_01_ Přechodové jevy v lineárních obvodech. Přerov, 2013.
AUTOR NEZNÁMÝ. Kapacita, induk č nost; kapacitor-kondenzátor, induktor-cívka [online]. [cit. 24.5.2015]. Dostupný na WWW: http://www.isibrno.cz/~joe/elektronika/elektronika_3.pdf

Obrázky

Obr. 1: BRINDL, Pavel. Derivační článek. VY_32_inovace_03_ELE_3_ Elektronické obvody_01_ Přechodové jevy v lineárních obvodech. Přerov, 2013.
Obr. 2: BRINDL, Pavel. Integrační článek. VY_32_inovace_03_ELE_3_ Elektronické obvody_01_ Přechodové jevy v lineárních obvodech. Přerov, 2013.
Obr. 3: BRINDL, Pavel. Přechodové charakteristiky integračního a derivačního článku. VY_32_inovace_03_ELE_3_ Elektronické obvody_01_ Přechodové jevy v lineárních obvodech. Přerov, 2013.
Obr. 4: BRINDL, Pavel. LAFCH derivačního článku. VY_32_inovace_03_ELE_3_ Elektronické obvody_01_ Přechodové jevy v lineárních obvodech. Přerov, 2013.
Obr. 5: BRINDL, Pavel. LAFCH integračního článku. VY_32_inovace_03_ELE_3_ Elektronické obvody_01_ Přechodové jevy v lineárních obvodech. Přerov, 2013.