Harmonická analýza

Definice

Harmonická analýza se zabývá matematickou teorií rozkladu periodického průběhu na jeho harmonické složky a způsobem určování těchto složek.

• Harmonická analýza  umožňuje rozepsat libovolný periodický průběh na součet sinusovek tzv. vyšších harmonických. Kmitočty jednotlivých harmonických jsou vždy celistvým násobkem kmitočtu původního signálu. Jednotlivé sinusové průběhy se liší kromě kmitočtu také amplitudou a vzájemným fázovým posuvem.
• Kmitočtová syntéza  je opakem harmonické analýzy . Výsledkem syntézy je tedy sečtení několika periodických signálů s různou amplitudou a frekvencí‚ čímž vznikne jeden jediný signál. Jak je zřejmé z jednoduchého součtu dvou sinusovek‚ je velmi důležité zachovat vzájemný fázový posuv.

Rozklad signálů na řadu harmonických odvodil v roce 1807 matematik J. J. Fourier. Proto se můžeme setkat také s výrazem Fourierova řada.              

Pro popis složitějšího signálu je třeba teoreticky nekonečno harmonických složek .Protože s rostoucím kmitočtem se amplituda harmonických zmenšuje, uvažují se při výpočtech pouze nižší členy Fourierovy řady. Platí‚ že pro zápis signálů se strmými branami (pila‚ obdélník) je zapotřebí více harmonických.

Vyšší harmonické                                                     

Matematicko-fyzikálně je dokázáno, že každý periodický střídavý sinusový průběh s frekvencí f lze rozložit na nekonečnou řadu (sinusových harmonických) průběhů s frekvencemi:

f₁ = 1 x f                 První (základní) harmonická

f₂ = 2 x f                 Druhá harmonická

f₃ = 3 x f                 Třetí harmonická
.
.
.

S amplitudami:
A₁
A₂
A₃
.
.
.

S fázemi:

φ₁

φ₂

φ₃
.
.
.

Sinusoidy s frekvencemi 2f, 3f … jsou tzv. vyšší harmonické:

Obr. 1: Vyšší harmonické

Skládání (superpozice) několika průběhů

Prochází-li lineárním bodem současně dva nebo více různých proudů, je okamžitá hodnota výsledného proudu dána algebraickým součtem jednotlivých proudů.

i = i₁ + i₂ + i₃

Pokud se jedná o napěťové zdroje (v lineárním obvodu):

u = u₁ + u₂ + u₃

Z hlediska výkonů:

P= u₀i₀ +u₁i₁ * cosφ₁ + u₂i₂ * cosφ₂ …….[W]

nultá                            efektivní
harmonická                hodnoty
složka                          jednotlivých
(ss složka)                   harmonických
 

Možné případy skládání sinusových průběhů

Skládání sinusových průběhů se stejnou frekvencí

• Vzájemný fázový posuv obou průběhů je 90° (sinová a kosinová složka)

Obr. 2: Vzájemný fázový posuv obou průběhů 90°

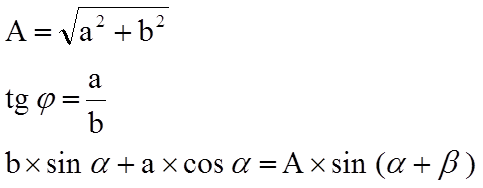
Každý sinusový průběh s amplitudou A a fázovým posuvem lze rozložit na sinusovou a kosinusovou složku:

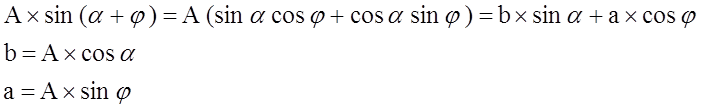
Vzájemný fázový posuv obou průběhů je obecně φ

Amplituda výsledného sinusového průběhu je dána kosinovou větou:

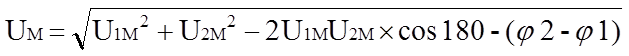
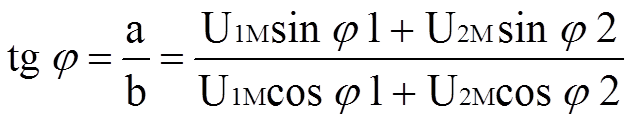
Skládání sinusových průběhů s různými frekvencemi

Skládají-li se dva sinusové průběhy s různými frekvencemi, je výsledný průběh periodický, ale nesinusový. Výsledný průběh závisí na velikosti amplitud skládaných průběhů a na rozdílnosti velikosti obou frekvencí.

Jednotlivé signály lze z tohoto výsledného signálu opět oddělit pomocí dolní a horní propusti s vhodně volenými mezními frekvencemi.  

• Skládání dvou sinusových průběhů, jejichž frekvence se značně liší (např. vf a nf napětí)

  Doba periody druhé složky signálu je několikanásobkem doby periody první složky signálu. Při pozorování takového výsledného signálu na osciloskopu lze zřetelně rozlišit jednotlivé frekvence.

  Jednotlivé signály lze z tohoto výsledného signálu opět oddělit pomocí dolní a horní propusti s vhodně volenými mezními frekvencemi.  

 

Obr. 3: Skládání dvou sinusových průběhů, jejichž frekvence se značně liší

• Skládání dvou sinusových průběhů, jejichž frekvence se liší jen málo

Jestliže sečteme dva signály s blízkými frekvencemi, u nichž se doba periody jen málo liší, můžeme použít následující úvahu: Předpokládejme, že v určitém okamžiku jsou signály ve fázi, jejich amplitudy se sčítají.

Po první periodě signálu s vyšší frekvencí je signál s nižší frekvencí o část periody zpožděn. V další periodě se zpoždění zvýší, za určitou dobu budou signály v protifázi, jejich amplitudy se odčítají. Pak se vzájemná fáze opět mění tak, že se signály sčítají ve fázi. Periodicky se mění výsledná amplituda signálu s frekvencí, vzniká zázněj.

Jestliže jsou amplitudy signálů stejné, amplituda se bude měnit podle druhého obrázku.

Frekvence zázněje se rovná rozdílu obou frekvencí.

            f_Z = f₁ - f₂

Obr. 3: Různé amplitudy obou signálů

Obr. 4: Stejné amplitudy obou signálů                                       

Zdroje

• [online]. [cit. 2014-08-23]. Dostupné z: www.isstechn.cz/objekty/analyza_signalu.doc

• AUTOR NEZNÁMÝ. Metody analýzy časově proměnných signálů [online]. [cit. 24.5.2015]. Dostupný na: www.souch.cz/dok/e/scitani.doc

• Harmonická analýza měření zkreslení. [online]. [cit. 2015-01-18]. Dostupné z: http://www.martin-n.estranky.cz/clanky/8_-maturitni-otazka.html

Obrázky

• Obr. 1: Vyšší harmonické. [online]. [cit. 2014-08-23]. Dostupné z: www.isstechn.cz/objekty/analyza_signalu.doc
• Obr. 2: Vzájemný fázový posuv obou průběhů 90°. [online]. [cit. 2014-08-23]. Dostupné z: www.isstechn.cz/objekty/analyza_signalu.doc
• Obr. 3: Různé amplitudy obou signálů. [online]. [cit. 24.5.2015]. Dostupný na: www.souch.cz/dok/e/scitani.doc
• Obr. 4: Stejné amplitudy obou signálů. [online]. [cit. 24.5.2015]. Dostupný na: www.souch.cz/dok/e/scitani.doc