Fourierův rozvoj

Definice - Fourierova věta

Každá jednoznačně určená periodická funkce, která má v intervalu konečný počet extrémů a nespojitostí, může být vyjádřena nekonečnou geometrickou řadou sinusových průběhů s amplitudami An, fázovými posuvy ϕn a úhlovou frekvencí ωn (kde „n“ je příslušná harmonická), které jsou celistvými násobky úhlové frekvence ω původní periodické funkce.

Fourierův rozvoj neboli amplitudový rozklad lze použít na každou jednoznačně určenou periodickou funkci F (t) s periodou T a frekvencí f mající v uzavřeném intervalu periodicity délky T jen konečný počet extrémů a nespojitostí prvého druhu.

Fourierův rozvoj

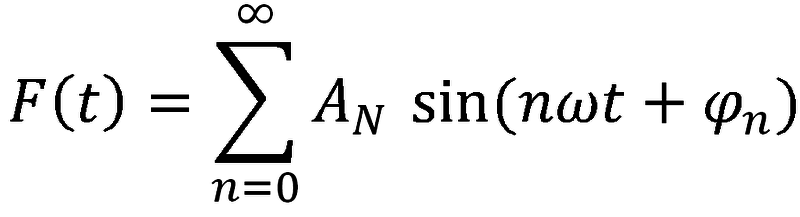
Každou sinusoidu s fázovým posuvem lze rozložit na součet složky sinusové a složky kosinusové.
Platí:

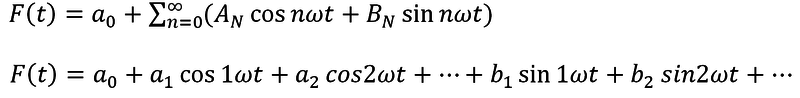
Pravé strany jsou goniometrické řady mající nekonečně mnoho členů. Tato řada se nazývá Fourierova řada.

Pro konkrétní vyjádření Fourierova rozvoje je nutné určit Fourierovy koeficienty.

Fourierovy koeficienty

A₀ = stejnosměrná složka

A_N = amplituda kosinové složky n-té harmonické

B_N = amplituda sinové složky n-té harmonické

 

Stanovení jednotlivých složek Fourierova rozvoje

- matematicky

- početně

- graficky

- harmonickým analyzátorem

Zjednodušení Fourierova rozvoje

V průběhu některých periodických signálů lze najít určité zákonitosti, které Fourierův rozvoj anulováním některých členů zjednoduší. Z tvaru křivky, která má analyzovaný průběh vyjadřovat, je možné zjednodušení dle těchto pravidel:

• Je-li průběh křivky souměrný dle počátku

platí: F(-t) = -F (t) – tzv. lichá funkce

Všechny kosinové složky jsou nulové, funkce F(t):

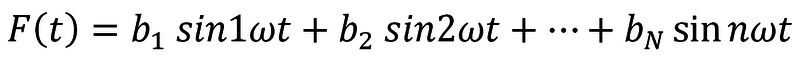
• Je-li křivka souměrná dle svislé osy

platí: F(-t) = F(t) – tzv. sudá funkce

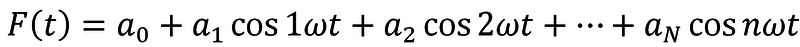
platí: F(t + T/2) = -F(t)

• Opakují-li se hodnoty v první polovině periody T a v druhé polovině s opačným znaménkem

platí: F(t + T/2) = -F(t)  F. rozvoj obsahuje pouze liché členy: Platí:

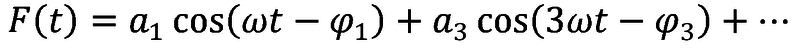
• Opakují-li se hodnoty v druhé polovině periody se stejným znaménkem

platí: F(t + T/2) = F(t).
F. rozvoj obsahuje jen sudé členy:

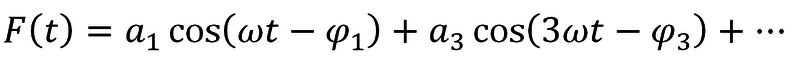
Frekvenční spektrum signálu

Vypočítáním hodnot Fourierových koeficientů a₀, a_n, b_n je výsledkem harmonické analýzy jednoznačně zapsané formou Fourierovy řady. Stejně jednoznačně a výstižně popisuje analyzovanou funkci frekvenční spektrum amplitud + frekvenční spektrum fází, popřípadě frekvenční spektrum kosinových složek spolu s frekvenčním spektrem sinusových složek.

Frekvenční spektrum amplitud je posloupnost amplitud A_N jednotlivých harmonických (diskrétní časové spektrum).

Délka úsečky znázorňuje velikost amplitudy příslušné harmonické (spektrální čára):

Obr. 1: Frekvenční spektrum signálu

Spektrum A_N je vždy kladné. Spektrum a_n, b_n, _a mohou být kladné i záporné.

Obr. 2: Průběh funkce a_n

Průběh funkce a_n = f (f) má tvar plynulé a zmenšující se sinusovky. Její průsečíky s vodorovnou osou jsou v bodech, kde příslušné harmonické mají nulovou amplitudu.

Energetický obsah spektra

Jednotlivé harmonické složky nemají stejné amplitudy, a proto ani výkon přenášený signálem není rozložen podél frekvenční osy rovnoměrně. Přibližně 90% celkové energie pravoúhlého signálu se přenáší složkami v prvním oblouku spektra. Složky druhého oblouku přenáší 50%, ve třetím 1,6% atd.

Harmonická syntéza

Jde o grafický součet jednotlivých harmonických složek. Je to zvláštní případ skládání sinusových průběhů s různými frekvencemi. Vyznačuje se tím, že skládané sinusoidy se shodnými amplitudami a se shodnými posuvy mají frekvence, které jsou celými násobky určité harmonické a vyšší harmonické a případně nulté harmonické čili stejnosměrné složky. Takto lze získat jakýkoliv periodický nesinusový průběh s frekvencí f, a pokud bude bez stejnosměrné složky, tak to bude periodický střídavý nesinusový průběh.

 

Zdroje

• KONVALINKA, Václav. Harmonická analýza [online]. [cit. 2014-08-23]. Dostupné z: konvav.czweb.org/prezentace/teorie/harmonicka_analyza.ppt

• [online]. [cit. 2014-08-23]. Dostupné z: www.isstechn.cz/objekty/analyza_signalu.doc

Obrázky

• Obr. 1: Frekvenční spektrum signálu. [online]. [cit. 2014-08-23]. Dostupné z: www.isstechn.cz/objekty/analyza_signalu.doc

• Obr. 2: Průběh funkce an. [online]. [cit. 2014-08-23]. Dostupné z: www.isstechn.cz/objekty/analyza_signalu.doc