Metody harmonické analýzy

Pro výpočet koeficientů Fourierovy řady se nejčastěji používá:

• Numerická metoda výpočtu

• Grafická metoda

• Rychlá Fourierova transformace (Fast Fourier Transform - FFT)

Numerická metoda výpočtu koeficientů Fourierovy řady

U průběhů získaných měřením bývá obtížné převést je na analytickou funkci. V takovém případě je možné řešení provést numericky. Při tomto způsobu nejprve rozdělíme periodu signálu 2π na konečný počet stejných dílků s velikostí Δx = 2π/c a v jejich koncových bodech určíme hodnoty funkce y_k. Tím vyjádříme spojitou funkcí konečným počtem hodnot, vzorků. Čím je větší počet dílků, tím je přesnější výsledek. Zároveň s tím se ale zvětšuje množství potřebných výpočtů.

Pro určení n harmonických musíme volit počet dílků c ≥ 2n + 2.

Nyní můžeme integrály pro výpočet koeficientů Fourierovy řady nahradit přibližným výpočtem výsledné plochy integrálu tím, že pro každý vzorek vynásobíme hodnotu funkce sinem nebo kosinem příslušného úhlu n ∙ x_k. Po vynásobení hodnotou Δx dostaneme plochu obdélníku o šířce Δx a výšce, který představuje hodnotu vypočtené funkce. Sečtením těchto obdélníčků získáme přibližnou hodnotu hledaného integrálu. Tato metoda se proto nazývá obdélníková.

Protože všechny obdélníky mají stejnou šířku, přejdou vzorce pro výpočet koeficientů na tvar:

,

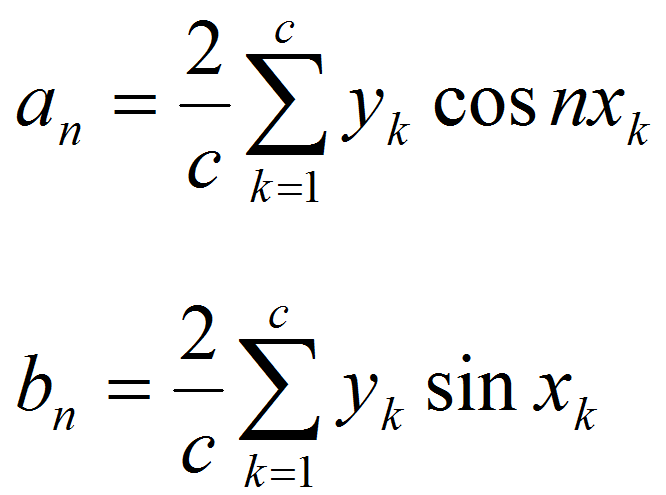Stejnosměrná složka bude:

,

 

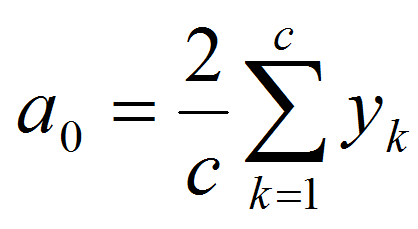Obr. 1: Rozdělení periody signálu

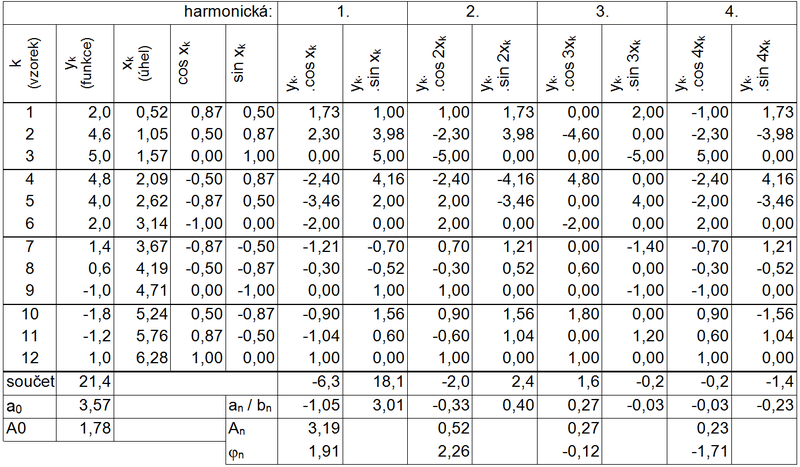
Je zřejmé, že bude nutné provést značný počet výpočtů, proto bude vhodné použít pro záznam výsledků tabulku, nebo přímo tabulkový kalkulátor.

Tabulka koeficientů

c =	12
D x	0,52	rad

 

Grafická metoda pro určení koeficientů Fourierovy řady

Přesnost této metody není velká, ale může usnadnit pochopení významu předchozích výpočtů a dalších úvah v následující metodě.
Především si uvědomíme, že vynásobení hodnoty funkce y_k sinem a kosinem příslušného úhlu vlastně určuje souřadnice koncového bodu vektoru délky y_k , natočeného v tomto úhlu. Součty jednotlivých složek lze vyjádřit graficky jako součet těchto vektorů.
Pro znázornění postupu použijeme předchozí průběh.

• Z grafu vybereme hodnoty y₁ až y₁₂ a znázorníme je jako vektory
• Připravíme hvězdici s dvanácti polopřímkami, s dělením po 60°
• Pro konstrukci koeficientů 1. harmonické vyneseme na tyto směry hodnoty y₁ až y₁₂ a provedeme jejich součet
• Pro konstrukci koeficientů 2. harmonické vyneseme hodnoty y₁ až y₁₂ postupně na směry s dvojnásobným úhlem a provedeme součet
• Amplitudu a fázi, případně kosinové a sinové složky určíme z výsledného vektoru, směřujícímu ke konci vektoru y₁₂.

Obdobný postup použijeme pro stanovení 3. a 4 harmonické.

 

Obr. 2: Hodnoty y1 až y12 jako vektory                                                                      

 

 

 

 

 

 

 

 

                                       Obr. 4: Hvězdice 2

 

 

 

Obr. 3: Hvězdice 1   
 

Rychlá Fourierova transformace (Fast Fourier Transform - FFT)

Fourierova transformace se provádí na určitém časovém úseku signálu, který obecně nemusí odpovídat době periody určitého periodického signálu. Jestliže zvolíme pro transformaci časový úsek, který právě odpovídá době periody, je výsledkem Fourierova řada.
Fourierova řada je tedy speciálním případem Fourierovy transformace.

Diskrétní Fourierova transformace je obdobou numerického výpočtu koeficientů Fourierovy řady. Transformovaný časový úsek T se rozdělí na N úseků, hodnoty funkce v koncových bodech těchto úseků se použijí pro výpočet amplitud příslušných složek. Frekvence těchto složek se však nevztahují k periodě signálu, ale k použitému časovému úseku T. 

Rychlá Fourierova transformace (FFT) je algoritmus výpočtu diskrétní Fourierovy transformace, který umožňuje snížit počet prováděných dílčích výpočtů a tím celý výpočet značně zrychlit. Úspora času je zvláště zřetelná u velkého počtu vzorků. Pro dosažení optimálního času výpočtu se měřený úsek dělí na počet stejných úseků, jejichž počet je roven právě mocnině 2 (např. 512 nebo 4098). Výsledkem transformace bude počet harmonických (odvozených od daného intervalu), který je polovinou počtu úseků (vzorků). Získané spektrum bude obsahovat nultou harmonickou (stejnosměrnou složku), frekvence první harmonické bude převrácenou hodnotou transformovaného intervalu a frekvence dalších harmonických budou celistvými násobky základní harmonické až do frekvence N/2T. 

Více na www.souch.cz/dok/e/scitani.doc.

 

Zdroje

• AUTOR NEZNÁMÝ. Metody analýzy časově proměnných signálů [online]. [cit. 24.5.2015]. Dostupný na: www.souch.cz/dok/e/scitani.doc

Obrázky

• Obr. 1: Rozdělení periody signálu. [online]. [cit. 24.5.2015]. Dostupný na: www.souch.cz/dok/e/scitani.doc

• Obr. 2: Hodnoty y1 až y12 jako vektory. [online]. [cit. 24.5.2015]. Dostupný na: www.souch.cz/dok/e/scitani.doc

• Obr. 3: Hvězdice 1. [online]. [cit. 24.5.2015]. Dostupný na: www.souch.cz/dok/e/scitani.doc

• Obr. 4: Hvězdice 2. [online]. [cit. 24.5.2015]. Dostupný na: www.souch.cz/dok/e/scitani.doc