MATEMATIKA

1) Vypočítejte:  a) kolik procent je 10 V z 200 V   

                                                              (5 %)

                       b) kolik procent je 5 mA ze 150 mA

                                                              (3,3 %)

                       c) kolik voltů je 1,5 % z 4,56 V

                                                              (0.0684 V)

2) Nakreslete pravoúhlý trojúhelník a vysvětlete význam goniometrických funkcí a Pythagorovy věty.

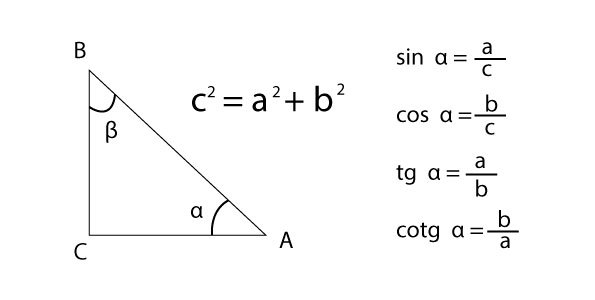
Obr. 1: Pravoúhlý trojúhelník

3) Nakreslete v Gaussově rovině komplexní číslo z = 5 + j10. Vyjádřete jej v goniometrickém a exponenciálním tvaru.

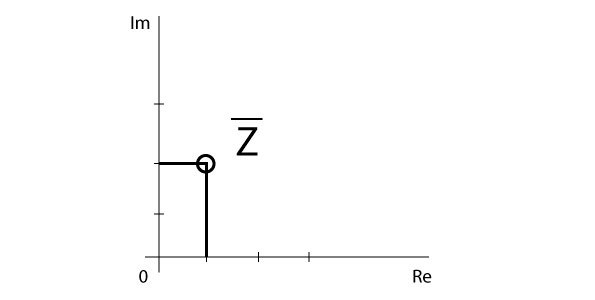
Obr. 2: Gaussova rovina

                                                            (z = 5√5·(cos1,1 + j sin1,1) = 5√5·e ^j1,1)

4) Vyřešte soustavu rovnic:

                   6 = x + 4·y

                  24 = 2·x + 2·y

                                                             (y = 2, x = 14)

ZÁKLADY ELEKTROTECHNIKY

1) Převeďte do daných jednotek:

                   20 mA =         µA             (20000)

                   0,1 kΩ =         MΩ            (0,0001)

                   12,5·10^-5 F =            nF          (125000)

                   28,5·10^-2 mA =         µA         (285)

2) Naučte se tabulku:

veličina	označení	jednotka
elektrický proud	I	A  ampér
intenzita el. pole	E	V/m  volt na metr
elektrický odpor	R	Ω  ohm
kapacita	C	F  farad
magnetická indukce	B	T  tesla
permitivita	ε	F/m  farad na metr
vlastní indukčnost	L	H  henry
fázový posuv	φ	rad  radián
jalový výkon	Q	var
reaktance	X	Ω  ohm

 

 

 

 

 

 

 

 

 

 

3) Nakreslete schéma zapojení nezatíženého děliče napětí R1 = 5 kΩ, R2 = 10 kΩ, U1 = 12 V. Vypočítejte proud děličem a napětí na jednotlivých rezistorech.

Obr. 3: Nezatížený dělič napětí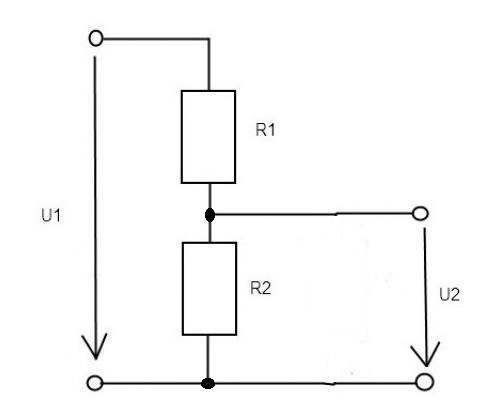

                                                              (I = 0,8 mA; U1 = 4 V; U2 = 8 V)

4) Nakreslete schéma zapojení zatíženého děliče napětí R1 = 1 kΩ, R2 = 2 kΩ, Rz = 2 kΩ, U = 100 V. Vypočítejte proud odebíraný ze zdroje a výstupní napětí děliče.

                                                                

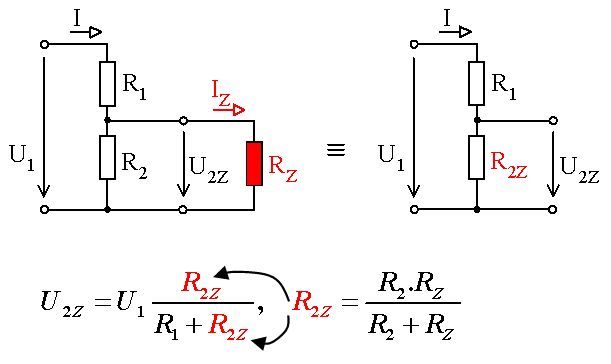
Obr. 4: Zatížený dělič napětí

                                                                (I = 50 mA, U_2Z = 50 V)

5) Zapojíme dva shodné kondenzátory C = 100 pF sériově (paralelně). Jaká je výsledná kapacita zapojení?

                        (sériově - jmenovitá kapacita je dělena počtem kondenzátorů, tj. 50 pF)

                        (paralelně - kapacity kondenzátorů se sčítají, tj. 200 pF)

6) Nakreslete schéma zapojení a fázorový diagram paralelního obvodu R, L, C.

                                                              

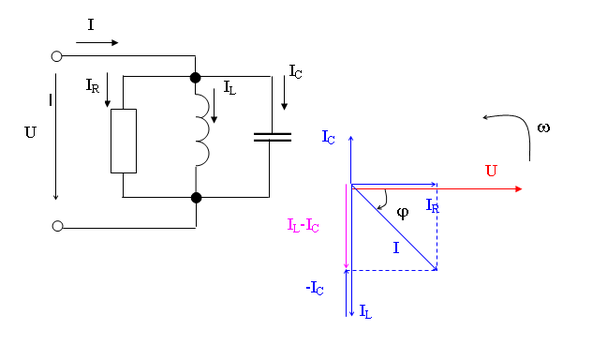
Obr. 5: Schéma zapojení a fázorový diagram obvodu RLC

ELEKTRONIKA

1) Vypište hodnoty řady jmenovitých hodnot E12.

                                                               (10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82)

2) Jak poznáte, že je proměnný rezistor lineární, logaritmický?

                                                                (N - lineární, G - logaritmický)

3) Vysvětlete základní parametry a konstrukční provedení kondenzátoru.

                                                                 (Kapacita - F, jmenovité napětí - U, otočný, vzduchový, papírový, elektrolytický, keramický, slídový, plastový)

ČÍSLICOVÁ TECHNIKA

1) Do časového diagramu zakreslete průběh výstupu funkce NOR.

                                                     

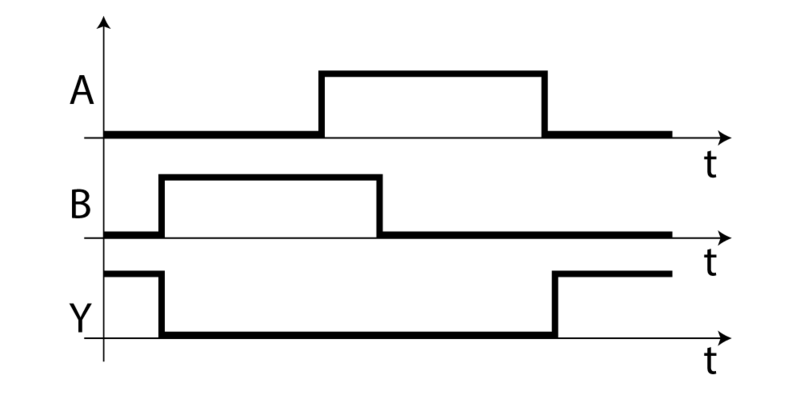
Obr. 6: Časový diagram

2) Pomocí hradel (dle ČSN) nakreslete schéma zapojení logické funkce V = not(A * notF) + G.

                                                     

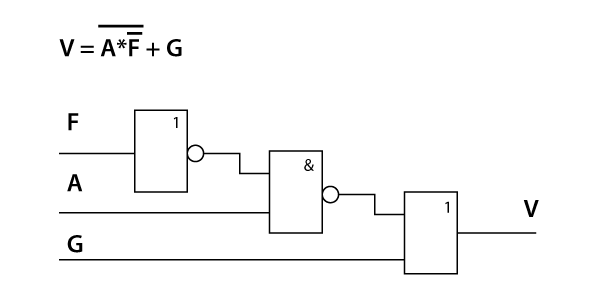
Obr. 7: Schéma zapojení logické funkce 

3) Nakreslete tabulku stavů a vypište výraz nezminimalizované logické funkce.

                                                       

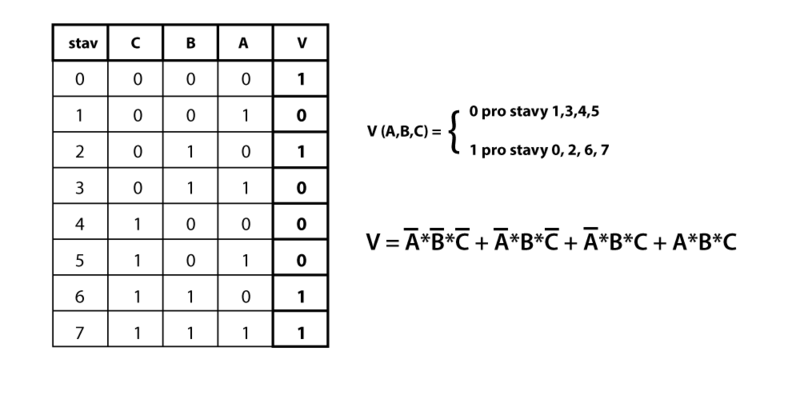
Obr. 8: Tabulka stavů

4) Předchozí logickou funkci minimalizujte pomocí Karnaughovy mapy.

                                                   

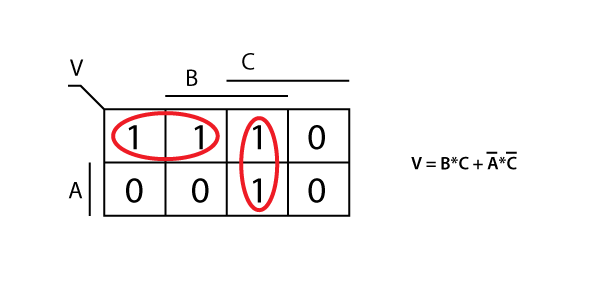
Obr. 9: Minimalizace funkce

 

Zdroje

• KYSELÝ, Libor. Elektrotechnická měření. Interní skriptum, VOŠ a SPŠE Olomouc. 2013

Obrázky

• Obr. 1 až Obr. 13: Archiv autora