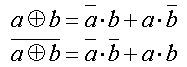Logické funkce

Úvod

Logické řízení – podobně jako činnost moderní digitální techniky – je založeno na zpracování a vyhodnocování dvouhodnotových neboli binárních signálů, které jsou časovým sledem dvou různých hodnot nebo stavů, například vypnutý/zapnutý, nevodivý/vodivý či nezmagnetovaný/zmagnetovaný. Symbolicky se dvouhodnotové veličiny vyjadřují hodnotami logická 0 a logická 1 či nepravda (F, false) a pravda (T, true), a jsou tedy analogické s proměnnými výrokové logiky – proto jsou vztahy mezi proměnnými nazývány logické funkce.

Řídicí obvody pracující na tomto principu se označují jako logické řídicí obvody. Většina řídicích systémů pracuje se spínanými signály a jedná se tedy o logické řídicí systémy. Logickými obvody máme dnes obvykle na mysli obvody elektronické, třebaže je lze realizovat také mechanicky, opticky, pneumaticky, hydraulicky či s využitím nanotechnologií a kvantové mechaniky.

Obr. 1: Mark I (1944). Plně automatické elektromechanické zařízení, které zvládlo tři základní operace za sekundu.

Samotné signály, nesoucí určitou informaci, označujeme jako logické proměnné. Ty jsou v digitální technice nejčastěji reprezentovány dvěma napěťovými úrovněmi – nižší úroveň L (z anglického low) odpovídá logické 0, vyšší úroveň H (z anglického high) zase logické 1. Vedle napětí, v závislosti na použité technologii, však může být logická hodnota vyjádřena také například prostřednictvím úrovně magnetizace či intenzity světelného toku.

Rovněž logické funkce, tedy předpisy, podle nichž jsou logické proměnné vyhodnocovány, mohou být pouze dvouhodnotové. Základní logické funkce jsou realizovány bezkontaktně pomocí logických členů (hradel) nebo kontaktně pomocí spínačů, relé a stykačů. Z těch se pak skládají veškeré složitější logické obvody a funkční bloky řídicích systémů.

Vyjádření logických funkcí

Přirozenému jazyku je nejbližší slovní vyjádření logické funkce, obsahující logické spojky.

„Žárovka je rozsvítí jen tehdy, jsou-li současně stisknuty oba spínače.“

„Poplach se spustí, je-li alarm aktivován a přitom dojde k rozbití okna nebo k pohybu ve vnitřním prostoru domu.“

Je zřejmé, že taková tvrzení jsou prakticky použitelná jen u jednodušších systémů, kde navíc nehrozí špatná interpretace živého jazyka. Proto existuje několik metod, jak logický systém popsat technicky správně a s možností dále jej upravovat – přesněji řečeno zjednodušovat. Každá z nich má své výhody, ale také svá omezení, obvykle daná počtem zpracovávaných logických proměnných. Mezi nejčastěji užívané formy popisu logické funkce patří:

a) pravdivostní tabulka

Pravdivostní tabulka tvoří model chování logického systému. Obsahuje všechny možné kombinace hodnot vstupních logických proměnných a jim náležící funkční hodnoty. Každé kombinaci odpovídá právě jedna hodnota logické funkce (logická 0, nebo logická 1). Počet možných kombinací, tedy řádků pravdivostní tabulky, je 2^N, kde N je počet logických proměnných.

Obsahuje-li logická funkce dvě proměnné, pravdivostní tabulka bude mít čtyři řádky pro kombinace vstupních hodnot 00, 01, 11. Pro tři proměnné se bude tabulka skládat z osmi řádků pro kombinace 000, 001, 010, 011, 100, 101, 110, 111. Pro čtyři proměnné bude mít řádků šestnáct. Při sestavování tabulky lze například postupovat tak, že hodnoty vstupních proměnných představují dvojková vyjádření celých čísel. (Vstupní proměnné se obvykle značí malými písmeny z počátku abecedy, logická funkce se označuje symbolem Y.)

Domovní alarm

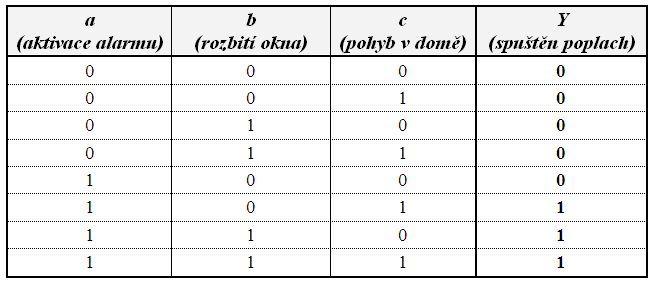
Domovní alarm spustí poplach, tedy vyhodnotí situaci stavem logické 1, je-li splněna následující kombinace podmínek:

• alarm je aktivován a přitom dojde k rozbití okna (a pohyb v domě není zaznamenán)

nebo

• alarm je aktivován (a není rozbito okno) a přitom je zaznamenán pohyb v domě

nebo

• alarm je aktivován a dojde k rozbití okna a také je zaznamenán pohyb v domě.

Informaci o splnění či nesplnění jednotlivých podmínek – tedy logické hodnoty vstupních logických proměnných – poskytují systému vhodná čidla. Větné spojky pak vytvářejí předpis – logickou funkci, kterou alarm zpracovává. Pravdivostní tabulka pro náš příklad se třemi proměnnými (aktivace alarmu, rozbití okna, pohyb v domě) bude obsahovat osm řádků se všemi kombinacemi vstupních logických hodnot a jim odpovídající odezvy systému alarmu:

Pokud pro některou kombinaci hodnot logických proměnných není určena funkční hodnota nebo pokud na ní v daném systému nezáleží, hovoříme o neúplně zadané logické funkci. Pak v příslušném řádku pravdivostní tabulky uvádíme symbol „X“. Ten pak při následném zjednodušování (minimalizaci) logické funkce – jak ukážeme později – můžeme využít buď jako logickou 0 nebo logickou 1, podle toho, co je pro získání minimálního logického systému výhodnější.

b) logický výraz

Logický výraz je modelem chování logického systému – hodnoty logické funkce získáme jeho vyhodnocením pro jednotlivé hodnoty vstupních proměnných. Kromě toho může být také modelem struktury logického systému – pomocí souboru kontaktních či bezkontaktních prvků lze podle něj sestavit logický obvod.

Zápis logického výrazu obsahuje – kromě logických proměnných a funkce – symboly logických spojek. Větné spojce „a současně“ (logickému součinu) odpovídá symbol „∙“, spojce „nebo“ (logickému součtu) symbol „+“ a tvrzení „není pravda, že“ (logická negace) se značí pruhem nad příslušnou proměnnou.

Zde je třeba zdůraznit, že všechny logické spojky jsou rovnocenné, tedy že například neexistuje přednost násobení před sčítáním známá z matematické algebry.

Náš příklad s domovním alarmem zapíšeme pomocí logického výrazu následovně:

„Poplach se spustí, je-li alarm aktivován a přitom dojde k rozbití okna nebo k pohybu ve vnitřním prostoru domu.“

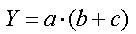
Z tabulky lze logický výraz vytvořit dvojím způsobem. Buď v podobě úplné součtové formy, kdy vybíráme pouze ty řádky, ve kterých je funkce pravdivá. Proměnné v daném řádku svážeme logickým součinem, přičemž má-li proměnná hodnotu logické 0, píšeme ji s negací – takto dostaneme takzvané mintermy. Následně všechny mintermy svážeme logickým součtem:

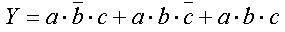
Všimněte si, že takto vzniklý logický výraz neodpovídá tomu, který jsme vytvořili na základě slovního předpisu. Důvodem je skutečnost, že pravdivostní tabulka poskytuje úplné termy, které musí být následně zjednodušeny (minimalizovány).

Součtová forma je výhodná tam, kde ve funkčních hodnotách převládají logické 0. V opačném případě lze vytvořit úplnou součinovou formu, rovnocennou formě součtové, kdy vybíráme pouze ty řádky tabulky, ve kterých je funkce nepravdivá. Proměnné v daném řádku svážeme logickým součtem, přičemž má-li proměnná hodnotu logické 1, píšeme ji s negací – takto dostaneme takzvané maxtermy. Následně všechny maxtermy svážeme logickým součinem:

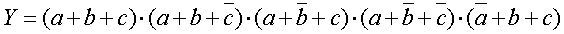
c) Karnaughova mapa

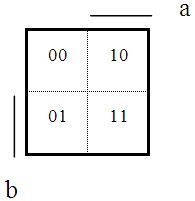
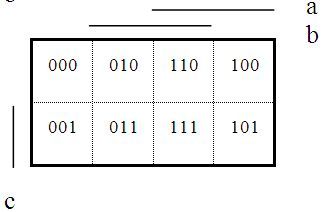
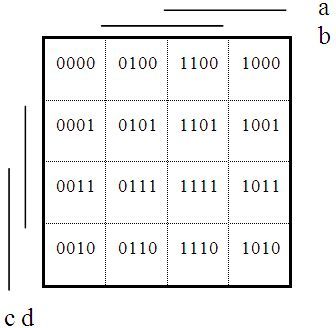
Karnaughova mapa je grafické vyjádření pravdivostní tabulky, kdy každému jejímu řádku odpovídá jedno pole mapy. Vodorovné i svislé rozměry mapy jsou rovny některé mocnině dvou. Logické proměnné tvoří souřadnice těchto polí a musí splňovat pouze jedinou podmínku: mezi dvěma sousedními poli se mění hodnota jen jedné souřadnice. (Sousední pole jsou ta, která se dotýkají hranou, svislou či vodorovnou, a rovněž pole na protilehlých okrajích mapy – jako bychom mapu „srolovali“, aby její levý okraj sousedil s pravým a současně dolní s horním.) Na rozvržení souřadnic tedy nezáleží. Má-li daná souřadnice hodnotu logické 1, značí se pruhem – který tentokrát nemá význam negace! Obsah jednotlivých polí představují hodnoty logické funkce (tedy i neurčité stavy) v příslušných řádcích pravdivostní tabulky.

V následujících ukázkách jsou do polí Karnaughových map pro dvě, tři a čtyři proměnné vepsány nejprve – pro snazší pochopení – pouze jejich souřadnice, tedy kombinace hodnot logických proměnných a, b, případně c a d.

Karnaughova mapa pro dvě proměnné a, b:

Karnaughova mapa pro tři proměnné a, b, c:

Karnaughova mapa pro tři proměnné a, b, c, d:

Vyjádření logické funkce naší úlohy s domovním alarmem pak jednoduše získáme tak, že v mapě pro tři proměnné nahradíme souřadnice jim odpovídajícími funkčními hodnotami:

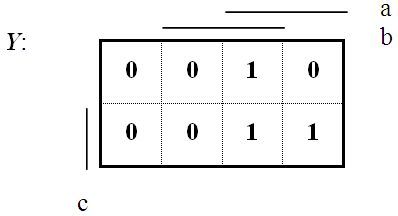
Karnaughovy mapy se s výhodou používají pro zápis logických funkcí pro tři a čtyři proměnné. Pro větší počet proměnných se však stávají méně přehlednými a bývají nahrazeny jinými způsoby vyjádření logických funkcí.

Základní logické funkce

V našem příkladu s domovním alarmem jsme si všimli tvrzení „alarm je aktivován a dojde k rozbití okna nebo k pohybu ve vnitřním prostoru domu“. To představuje složený výrok, který je vytvořen z několika výroků jednoduchých pomocí větných spojek. Jeho pravdivost je vyhodnocována pomocí logické funkce, tedy předpisu, který obsahuje vstupní logické proměnné vázané logickými spojkami. Obvykle se skládá z několika základních logických funkcí jedné či dvou logických proměnných.

Logické funkce lze nejsnáze zapsat pomocí logických výrazů, které se řídí pravidly booleovské – tedy nikoli matematické – algebry: jednotlivé logické proměnné jsou obvykle označovány malými písmeny z počátku abecedy, logické funkce pak symbolem Y.

a) logický součet (logická funkce OR)

Logický součet popisuje tvrzení, které je vyhodnoceno jako pravdivé, je-li splněna alespoň jedna ze vstupních podmínek. Nebo – které je vyhodnoceno jako nepravdivé pouze v případě, kdy jsou obě (všechny) vstupní podmínky nepravdivé. Značí se spojkou OR (z anglického nebo) a představuje vlastně množinovou disjunkci. V Booleově algebře jí přísluší znaménko „+“, takže celý výrok pro dvě logické proměnné zapisujeme a + b = Y. Znaménko logického součtu má ovšem jiný význam než v klasické algebře: sice 0 + 0 = 0 a také 1 + 0 = 0 + 1 = 1, ale 1 + 1 = 1 (což značí případ, kdy jsou splněny obě vstupní podmínky současně). Proto jej nečteme jako „plus“, ale jako „nebo“. Pravdivostní tabulkou lze funkci logického součtu popsat takto:

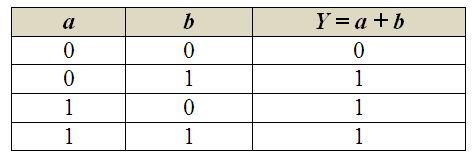
b) logický součin (logická funkce AND)

Logický součin popisuje tvrzení, které je vyhodnoceno jako pravdivé, jsou-li splněny obě (všechny) vstupní podmínky současně. Nebo – které je vyhodnoceno jako nepravdivé, pokud alespoň jedna vstupní podmínka splněna není. Značí se spojkou AND (z anglického a současně) a představuje množinovou konjunkci. V Booleově algebře jí přísluší znaménko „∙“, takže celý výrok pro dvě logické proměnné zapisujeme a ∙ b = Y, případně ab = Y. Znaménko logického součinu se tentokrát od matematického „krát“ neliší, přesto jej budeme číst jako „a“, „i“ či „a současně“. Pravdivostní tabulka popisuje funkci logického součinu následovně:

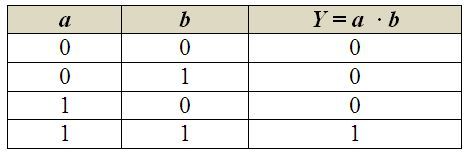
c) logická negace (logická funkce NOT)

Nejjednodušší z logických funkcí je logická negace. Na rozdíl od předešlých se jedná o funkci jedné proměnné. Logická negace je pravdivá, je-li vstupní podmínka nepravdivá – a obráceně. Výsledkem této funkce je tedy opačná hodnota. Značí se spojkou NOT a v Booleově algebře se zapisuje pruhem nad příslušnou logickou proměnnou: ā = Y. Pravdivostní tabulka je zřejmá:

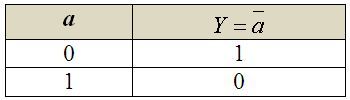
Úplný systém logických funkcí

Předchozí tři logické funkce společně tvoří takzvaný úplný systém logických funkcí, což znamená, že pouze pomocí nich lze vyjádřit jakoukoli logickou funkci, a tedy i realizovat libovolné, byť sebesložitější logické zařízení. A to může být v praxi velmi výhodné, neboť nepotřebujeme širokou škálu hradel, kterými jsou základní logické funkce implementovány.

d) negovaný logický součet (logická funkce NOR)

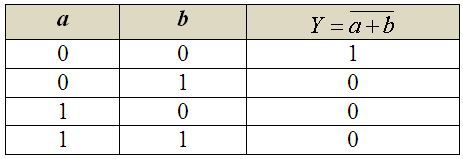
Negovaný logický součet, v matematice označovaný jako Piercova funkce, popisuje tvrzení, které je vyhodnoceno jako pravdivé pouze v případě, jsou-li obě (všechny) vstupní podmínky nepravdivé. Nebo – které je nepravdivé, je-li splněna alespoň jedna ze vstupních podmínek. Značí se spojkou NOR (NOT OR) a v Booleově algebře se zapisuje negací nad logickým součtem: 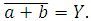Pravdivostní tabulkou lze tuto funkci popsat takto:

e) negovaný logický součin (logická funkce NAND)

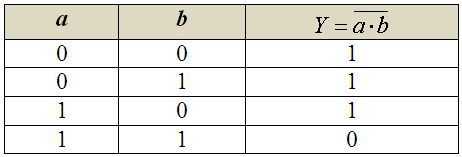
Negovaný logický součin, v matematice známý jako Shefferova funkce, popisuje tvrzení, které je vyhodnoceno jako pravdivé pouze v případě, je-li alespoň jedna vstupní podmínka nepravdivá. Nebo – které je nepravdivé pouze tehdy, jsou-li splněny obě (všechny) vstupní podmínky. Označuje se spojkou NAND (NOT AND) a v Booleově algebře se zapisuje negací nad logickým součinem: 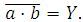Pravdivostní tabulka tuto funkci popisuje takto:

Samotná funkce NAND i samotná funkce NOR tvoří rovněž úplné systémy logických funkcí, takže pouze jejich vhodným zapojením lze realizovat libovolnou logickou funkci. Tato skutečnost je výhodná především technologicky, neboť moderní polovodičová hradla obou funkcí mají jednoduchou strukturu a představují elementární prvky pro hradla ostatních funkcí.

Následující dvě logické funkce, doslovně vzato, již tedy mezi základní nepatří, neboť je lze vyjádřit pomocí některého z výše uvedených úplných systémů logických funkcí. Přesto si je zde popíšeme, neboť jejich význam – porovnání obou vstupních hodnot logických proměnných – lze uplatnit v řadě logických obvodů.

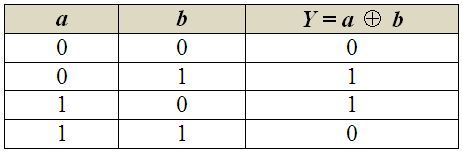
f) výlučný logický součet (logická funkce XOR)

Výlučný logický součin, či také nonekvivalence, popisuje tvrzení, které je vyhodnoceno jako pravdivé, jsou-li logické hodnoty obou vstupních proměnných různé. Neboli – je-li pravdivá právě jedna ze vstupních proměnných. Značí se spojkou XOR (eXclusive OR, tedy anglické buď - anebo) a v Booleově algebře jí přísluší znaménko „⊕“, takže výrok zapisujeme a ⊕ b = Y. Pravdivostní tabulkou lze funkci výlučného logického součtu popsat takto:

g) negovaný výlučný logický součet (logická funkce XNOR)

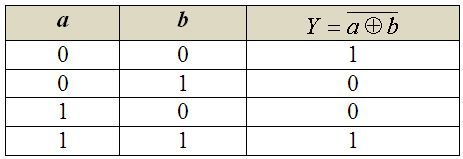
Negovaný výlučný logický součet neboli ekvivalence popisuje tvrzení, které je vyhodnoceno jako pravdivé, jsou-li logické hodnoty obou vstupních proměnných shodné. Značí se spojkou XNOR (eXclusive NOR) a v Booleově algebře se zapisuje negací nad výlučným logickým součtem: 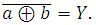Pravdivostní tabulka popisuje funkci logického součinu následovně:

Jak jsme již uvedli výše, logické XOR a XNOR lze vyjádřit a realizovat pomocí některého z úplných systémů logických funkcí – například funkcemi AND, OR a NOT. Lze ukázat, že platí následující rovnosti:

Zdroje

• Autor neznámý. mikrokontrolery-pic.cz [online]. [cit. 2014-2-12]. Dostupný na www: http://mikrokontrolery-pic.cz/zaciname/cislicova-technika/logicke-obvody/

Obrázky

• Obr. 1: Autor neznámý. rhizome.org [online]. [cit. 2014-2-16]. Dostupný na www: http://rhizome.org/editorial/2013/apr/9/queer-history-computing-part-three/