Laplaceova transformace

V teorii automatického řízení je Laplaceova transformace účinným nástrojem při popisu chování spojitých lineárních obvodů. Usnadňuje řešení lineárních diferenciálních rovnic.

Laplaceova transformace převádí funkce reálné proměnné t (časové funkce) na funkce komplexní proměnné tzv. operátoru s=α+jω (používá se i označení p). Časovou funkci označujeme jako originál, transformací získáme obraz. Umožňuje převést diferenciální rovnici n-tého řádu na algebraickou n-tého stupně a vytvoření obrazového přenosu jako jednoho ze způsobů vyjádření dynamických vlastností.

Transformace časové funkce f(t) na funkci komplexní proměnné F(s)se provádí pomocí definičního integrálu Laplaceovy transformace:

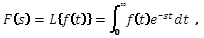
kde f(t) je originál a F(s) je obraz.

Příklad 1.

Vypočítejte Laplaceův obraz jednotkového skoku 1(t).

Jednotkový skok je definován

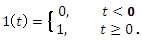
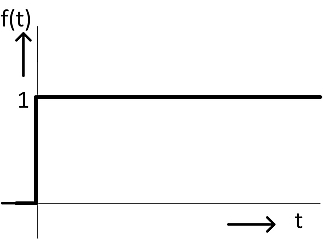
 Obr. 1: Jednotkový skok

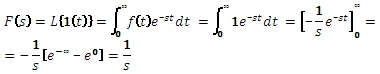
Příklad 2.

Vypočítejte Laplaceův obraz exponenciální funkce .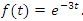

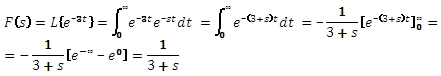
V praxi využijeme pro získání obrazu funkce slovník Laplaceovy transformace, ve kterém najdeme obrazy často se vyskytujících funkcí.

Ve slovníku zjistíme, že derivování se převádí na násobení operátorem s:

               originál                                                      obraz

Postup při použití Laplaceovy transfomace:

Diferenciální rovnici (originál) převedeme pomocí slovníku na obraz, úlohu řešíme v obraze a pokud je to vyžadováno, tak výsledek převedeme zpětnou Laplaceovou transformací L^-1 do originálu, opět s využitím slovníku.

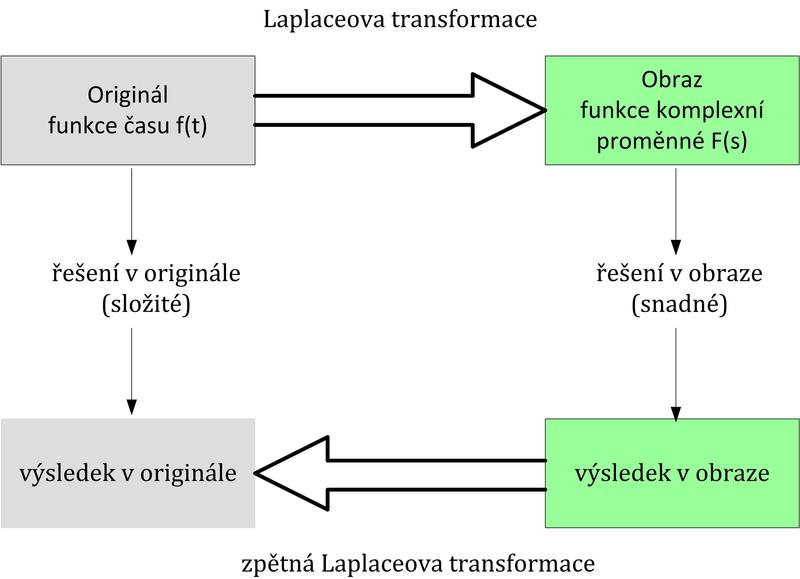
   Obr. 2: Postup při použití Laplaceovy transformace