Derivační členy

Výstupní signál x₂(t) je úměrný derivaci vstupního signálu x₁(t), tedy  velikost výstupního signálu je přímo úměrná rychlosti, kterou se mění vstupní signál.

Ideální derivační člen

Ideální derivační člen nevykazuje setrvačnost.

Diferenciální rovnice:

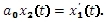
Po úpravě

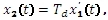
kde  

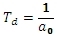
je derivační časová konstanta.

Z obrazu rovnice v transformaci  

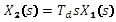
vyjádříme obrazový přenos:

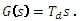
Frekvenční přenos je

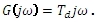
Přechodová charakteristika má tvar Diracova impulzu zvětšeného T_d krát:

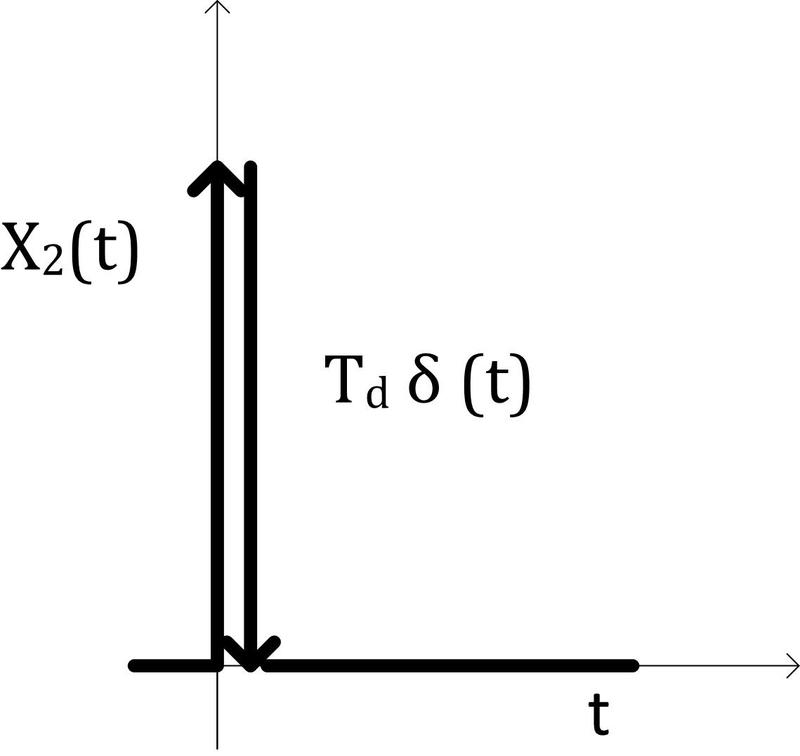
Obr. 1: Přechodová charakteristika ideálního derivačního členu

Frekvenční přenos je ryze imaginární a amplituda roste s frekvencí, proto frekvenční charakteristika splývá s kladnou částí imaginární osy:

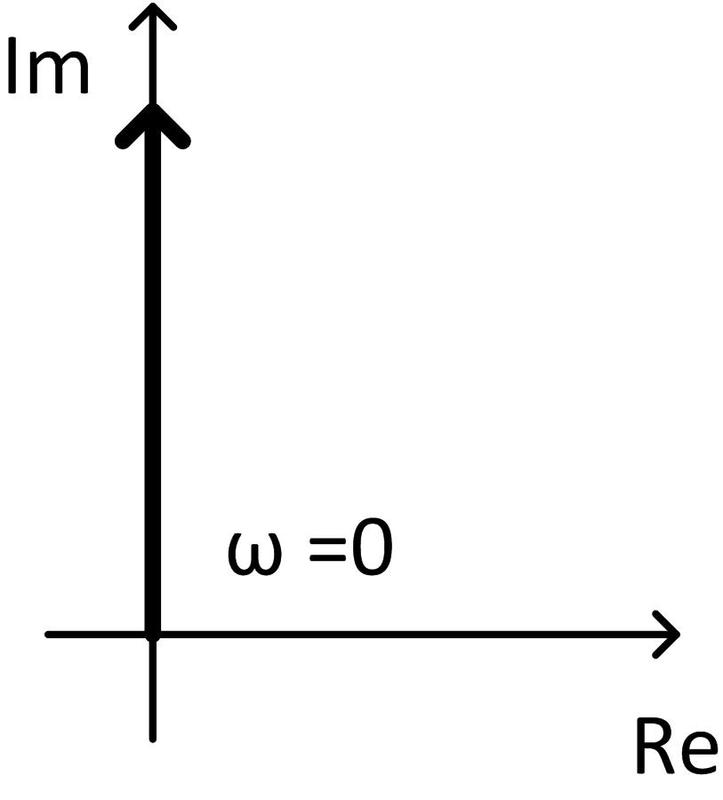
Obr. 2: Frekvenční charakteristika ideálního derivačního členu

Ideální derivační člen nelze realizovat. Skutečný derivační člen je vždy zatížen setrvačností. Je tvořen sériovým spojením ideálního derivačního členu a setrvačného členu s časovou konstantou T.

Derivační člen se setrvačností 1. řádu

Diferenciální rovnice:

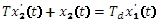
Obrazový přenos:

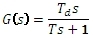
A frekvenční přenos:

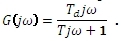
Přechodová a frekvenční charakteristika:

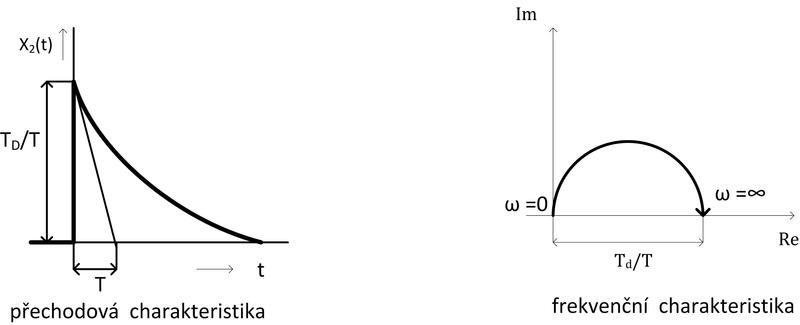
Obr. 3: Charakteristiky derivačního členu se setrvačností

Jako model můžeme použít CR obvod (derivační článek):

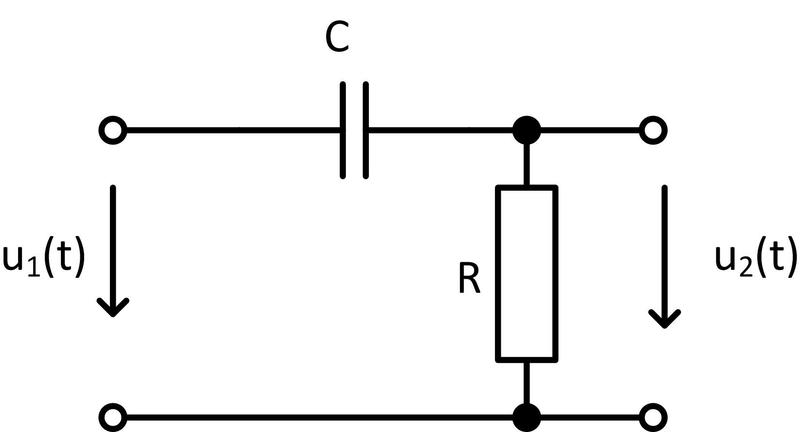
Obr. 4: Model derivačního členu

Příklad: Sestavte diferenciální rovnici nezatíženého derivačního článku.

Podle 2. Kirchhoffova zákona platí:

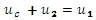
Pro napětí na kondenzátoru platí:

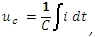
Pokud je článek nezatížený, neprotéká odbočkou proud a kondenzátorem protéká stejný proud jako rezistorem:

takže napětí na kondenzátoru můžeme vyjádřit jako

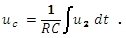
Dosadíme do rovnice a rovnici derivujeme:

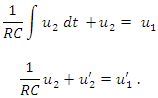
Po úpravě získáme tvar

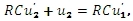
který odpovídá diferenciální rovnici derivačního členu se setrvačností 1.řádu, když T=T_d=RC .

Zdroje

• BALÁTĚ, Jaroslav. Automatické řízení. 2. přepracované vyd. Praha: BEN – technická literatura, 2004, 664s. ISBN 80-7300-148-9

• VORÁČEK, Rudolf, František ANDRÝSEK, Zdeněk BRÝDL, Luděk KOHOUT a Ladislav ŠMEJKAL. Automatizace a automatizační technika II. 1.vyd. Praha: Computer Press, 2000, 218s. ISBN 80-7226-247-5

Obrázky

• Obr. 1, 2, 3 a 4: Archiv autora