Přenosy regulačního obvodu, charakteristická rovnice

Regulace probíhá v uzavřeném regulačním obvodu, který vznikne připojením regulátoru k regulované soustavě.

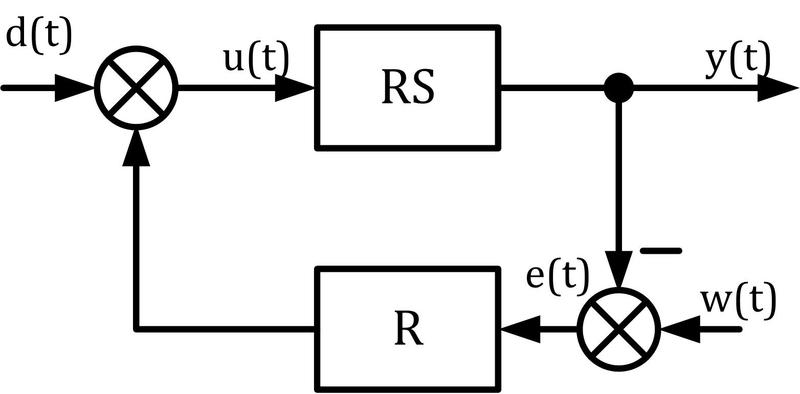
Obr. 1: Blokové schéma jednoduchého regulačního obvodu

Pro zkoumání vlastností celého obvodu potřebujeme znát jeho celkový přenos. Nejčastěji stanovujeme přenos řízení a přenos poruchy.

Přenos řízení

Přenos řídící veličiny určujeme za těchto podmínek:

• vstupní veličina je w(t)
• výstupní veličina je y(t)
• poruchy d(t)=0.

Blokové schéma uzavřeného obvodu podle podmínek upravíme a podle pravidel blokové algebry určíme přenos obvodu.

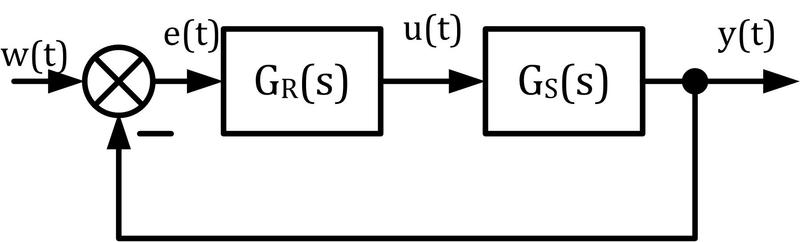
Obr. 2: Schéma pro určení přenosu řízení

Přenos řízení:

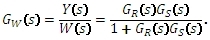
Pokud rozpojíme zpětnou vazbu, dostaneme otevřený regulační obvod, jehož přenos je:

 

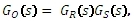
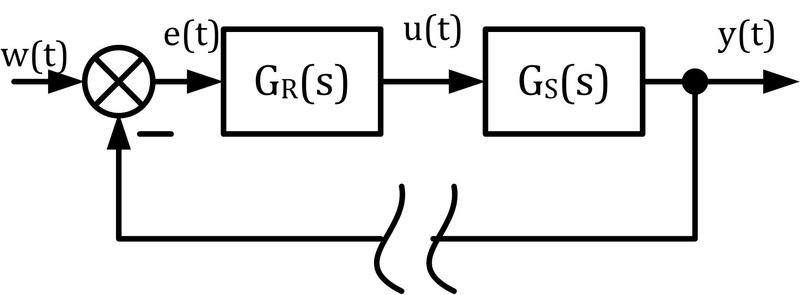
Obr. 3: Schéma otevřeného regulačního obvodu

takže můžeme přenos řízení zapsat také ve tvaru:

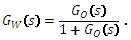
Přenos poruchy

Podmínky pro stanovení:

• vstupní veličina je d(t)
• výstupní veličina je y(t)
• řídící veličina w(t) =0.

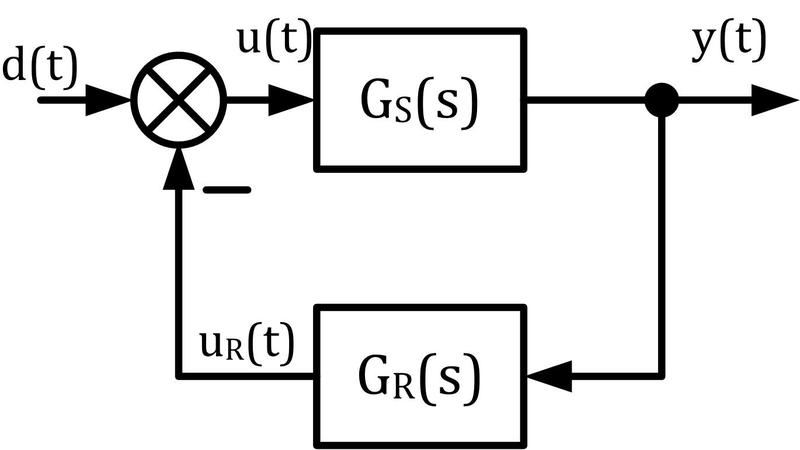
Obr. 4: Schéma pro určení přenosu poruchy

Přenos poruchy:

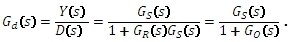
Charakteristická rovnice

Oba přenosy mají stejný jmenovatel. Pokud dosadíme konkrétní přenosy regulátoru a regulované soustavy, tak ve jmenovateli získáme charakteristický polynom a pokud jej položíme rovný nule, obdržíme charakteristickou rovnici regulačního obvodu:

Úloha:

Vypočítejte přenos řízení regulačního obvodu, který je tvořen regulovanou soustavou s přenosem

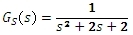
a regulátorem s přenosem

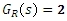
a zapište charakteristickou rovnici obvodu.

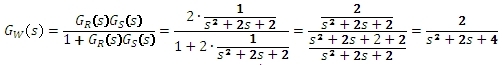
Charakteristická rovnice obvodu:

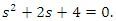
Charakteristická rovnice je určující pro řešení stability regulačního obvodu. Regulační obvod je stabilní, jestliže se při libovolné změně vstupní veličiny po odeznění přechodného děje výstupní veličina ustálí na nové hodnotě. Stabilita je nutnou podmínkou správné činnosti regulačního obvodu.

Pokud je obvod stabilní, mají všechny kořeny charakteristické rovnice zápornou reálnou část, tj. leží v levé polorovině komplexní roviny. V tom případě mají všechny koeficienty charakteristické rovnice stejné znaménko a žádný není roven nule. Pro rovnici druhého stupně je to postačující podmínka, u rovnic vyššího stupně musíme rovnici řešit nebo použít některé z kritérií stability, která umožňují rozhodnout o stabilitě obvodu bez výpočtu kořenů.

Příklady:

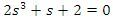
- obvod nestabilní, protože chybí koeficient a₂

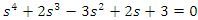
- obvod nestabilní, koeficient a₂ má jiné znaménko než ostatní koeficienty

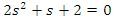
- obvod stabilní, všechny koeficienty mají stejné znaménko a rovnice je 2. stupně

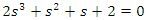
- všechny koeficienty mají stejné znaménko a jsou nenulové (podmínka nutná), ale stabilitu je potřebné dále řešit

 

Zdroje

• BALÁTĚ, Jaroslav. Automatické řízení. 2. přepracované vyd. Praha: BEN – technická literatura, 2004, 664s. ISBN 80-7300-148-9.
• VORÁČEK, Rudolf, František ANDRÝSEK, Zdeněk BRÝDL, Luděk KOHOUT a Ladislav ŠMEJKAL. Automatizace a automatizační technika II. 1.vyd. Praha: Computer Press, 2000, 218s. ISBN 80-7226-247-5.

Obrázky

• Obr. 1, 2, 3 a 4: Archiv autora