Michajlovovo-Leonhardovo kritérium

Michajlovovo kritérium stability patří mezi frekvenční kritéria, která posuzují stabilitu podle průběhu charakteristik (grafická kritéria). Může být použito i v obvodech s dopravním zpožděním.

Vychází z charakteristického polynomu, do kterého za operátor s dosadíme výraz jω. Tak získáme tzv. Michajlovovův vektor a jeho znázorněním v komplexní rovině Michajlovovu charakteristiku.

Definice: Uzavřený regulační obvod je stabilní, když Michajlovova charakteristika začíná na kladné reálné poloose a při změně úhlové frekvence ω od 0 do ∞ prochází tolika kvadranty, kolikátého stupně je charakteristický polynom. Průchod kvadranty musí být v kladném smyslu, tj. proti směru pohybu hodinových ruček.

Příklad:

Obr. 1: Průběhy Michajlovových charakteristik pro různé případy

Úloha 1.

Vyšetřete stabilitu Michajlovovým kritériem, je-li charakteristická rovnice obvodu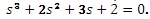

Do charakteristického polynomu 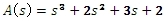dosadíme s=jω:

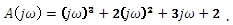
Michajlovovův vektor upravíme a rozdělíme na reálnou a imaginární část:

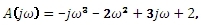
reálná část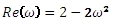

a imaginární část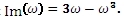

Pro zvolené hodnoty ω vypočítáme body charakteristiky a charakteristiku zakreslíme do komplexní roviny (lze využít např. excel).

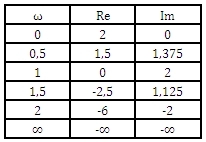
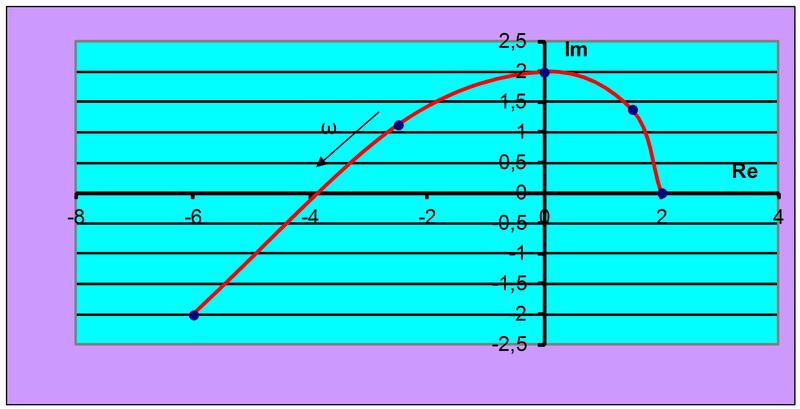
Obr. 2: Řešení úlohy 1

Obvod je stabilní, protože charakteristika začíná na kladné reálné poloose a prochází postupně v kladném smyslu třemi kvadranty.

Úloha 2.

Zkontrolujte stabilitu obvodu, jestliže charakteristický polynom má tvar

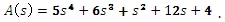
(volte ω = 0; 1; 2)

Výsledek: Obvod je nestabilní.

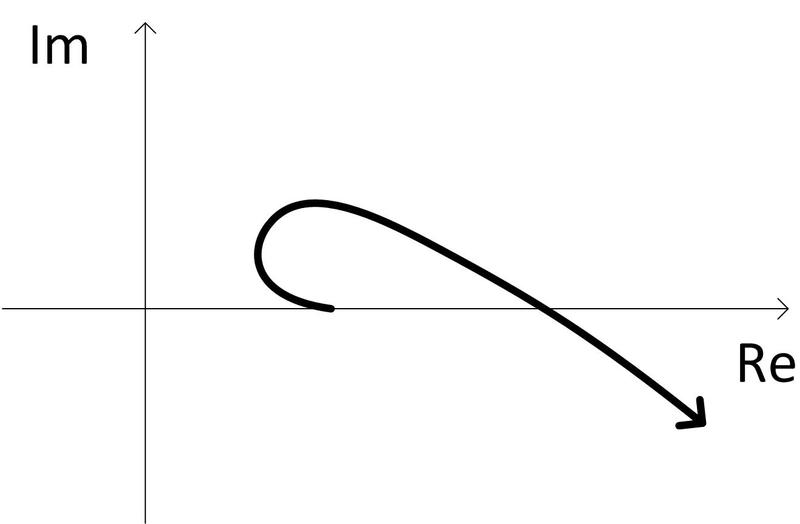
Obr. 3: Přibližný tvar Michajlovovy charakteristiky k úloze 2

 

Zdroje

• BALÁTĚ, Jaroslav. Automatické řízení. 2. přepracované vyd. Praha: BEN – technická literatura, 2004, 664s. ISBN 80-7300-148-9.

Obrázky

• Obr. 1, 2 a 3: Archiv autora