Nejmarkovo kritérium

Nejmarkova metoda umožňuje vymezení oblasti, ve které se může měnit zvolený stavitelný parametr regulátoru (k_R, T_i, T_d) při dodržení podmínek stability regulačního obvodu. Pracuje s charakteristickou rovnicí ve frekvenční oblasti.

Postup: Charakteristickou rovnici převedeme do frekvenční oblasti dosazením s=jω. Z rovnice vyjádříme hledaný parametr a získaný výraz rozdělíme na reálnou a imaginární část. Za ω dosazujeme postupně hodnoty od -∞ do +∞. Z vypočtených bodů sestrojíme křivku v komplexní rovině ( obraz imaginární osy komplexní roviny kořenů charakteristické rovnice). Křivka je pro kladné a záporné hodnoty ω souměrná kolem reálné osy.

Oblast stability leží vlevo od křivky při postupu ve smyslu stoupající frekvence ω od -∞ do +∞. Protože hledaný parametr je reálné číslo, může nabývat hodnot v úseku vyznačeném šipkou na reálné ose.

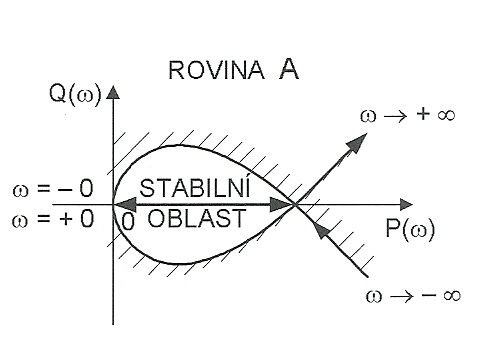
Obr. 1: Rozdělení komplexní roviny parametru A na stabilní a nestabilní oblast

Příklad:

Nejmarkovým kritériem zjistěte, v jakých mezích můžeme nastavovat zesílení regulátoru, aby obvod zůstal stabilní:

Charakteristickou rovnici můžeme získat např. z přenosu poruchy:

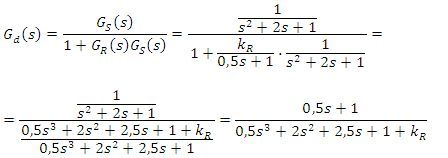
Charakteristická rovnice: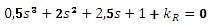

Dosadíme s=jω:

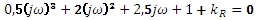
Upravíme a vyjádříme k_R:

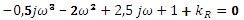
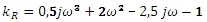
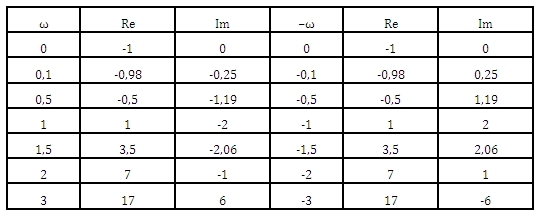
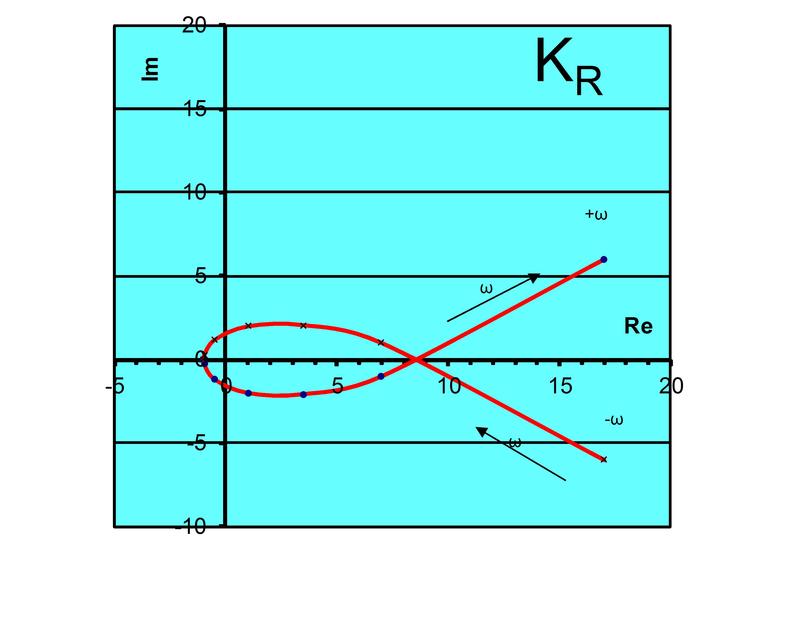
Obr. 2: Řešení příkladu

Z charakteristiky vyplývá, že k_R můžeme nastavovat od 0,5 do 8.

Úloha:

V jakých mezích můžeme nastavovat zesílení regulátoru v obvodu s charakteristickou rovnicí:

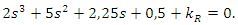
Doporučené hodnoty ω=0; 0,5; 1; 1,1

Výsledek: k_R může být voleno od 0,5 do 5.

 

Zdroje

• BALÁTĚ, Jaroslav. Automatické řízení. 2. přepracované vyd. Praha: BEN – technická literatura, 2004, 664s. ISBN 80-7300-148-9

Obrázky

• Obr. 1: BALÁTĚ, Jaroslav. Automatické řízení. 2. přepracované vyd. Praha: BEN – technická literatura, 2004, 664s. ISBN 80-7300-148-9.
• Obr. 2: Archiv autora