Minimalizace logických funkcí

Logický výraz představuje model struktury logického systému – každá operace přestavuje jeden jeho realizační prvek, tedy logické hradlo u bezkontaktní realizace nebo stykač či relé u kontaktní realizace, každá proměnná pak reprezentuje jeden vstup těchto realizačních prvků.

Pro účelnou realizaci logické funkce je proto třeba vyjádřit ji co nejjednodušším ekvivalentním logickým výrazem – zadanou logickou funkci je třeba minimalizovat. Minimalizace, kromě jiného, přináší jednodušší technologický proces a vyšší spolehlivost logického systému.

Kriteria minimalizace

Bez ohledu na zvolenou metodu minimalizace je vždy třeba usilovat o:

• minimální počet logických operací (tj. počet realizačních prvků)

• minimální počet proměnných (tj. počet vstupů realizačních prvků)

• kombinaci obou předchozích kriterií pro zvolený (či danou technologií dovolený) soubor realizačních prvků.

Booleova algebra

Logickou algebru vytvořil v roce 1854 irský matematik George Boole. Jedná se o soustavu pravidel určených k popisu vztahů mezi logickými proměnnými. Vzhledem k tomu, že argumenty logických proměnných nabývají pouze dvou hodnot, logické 0 či logické 1, je třeba Booleovu algebru chápat nikoliv jako algebru čísel, ale jako algebru stavů.

Zákony Booleovy algebry budeme používat při minimalizaci logických funkcí. Všechny mají dvojí formu – součtovou a součinovou, které jsou duální, to znamená, že jedna forma vyplývá z druhé při záměně logického součtu (OR) za logický součin (AND) a současně hodnoty logické 0 za logickou 1.

Na tomto místě je třeba připomenout, že logické spojky jsou rovnocenné, tedy že neexistuje přednost násobení před sčítáním známá z matematické algebry.

	Součtová forma	Součinová forma
Axiomy	0 + 0 = 0	1 · 1 = 1
	0 + 1 = 1 + 0 = 1	1 · 0 = 0 · 1 = 0
	1 + 1 = 1	0 · 0 = 0
Zákon komutativní	a + b = b + a	a · b = b · a
Zákon asociativní	a + (b + c) = (a + b) + c	a · (b · c) = (a · b) · c
Zákon distributivní	(a · b) + (a · c) = a · (b + c)	(a + b) · (a + c) = a + (b · c)
Zákon idempotence	a + a = a	a · a = a
Zákon vyloučeného třetího	a + ā = 1	a · ā = 0
Zákon agresivních hodnot	a + 1 = 1	a · 0 = 0
Zákon neutrálních hodnot	a + 0 = a	a · 1 = a
Zákon adsorpce	a + a · b = a	a · (a + b) = a
Zákon adsorpce negace	a + ā · b = a + b	a · (ā + b) = a · b
Zákon dvojí negace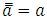
Zákony deMorganovy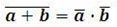

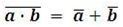Minimalizace výrazů s využitím Booleovy algebry

Na několika příkladech si ukážeme, jak lze s využitím zákonů Booleovy algebry minimalizovat logické funkce. Obvykle, ne však nutně vždy, pracujeme se součtovou formou logické funkce, tedy se součtem mintermů získaným z pravdivostní tabulky.

Příklad 1:

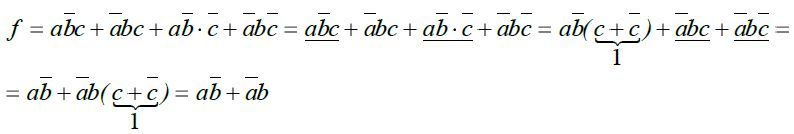
Příklad 2:

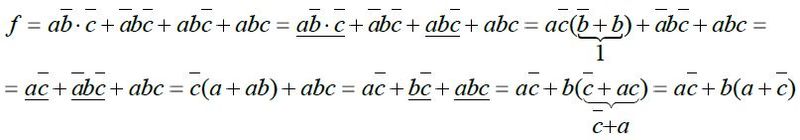
Příklad 3:

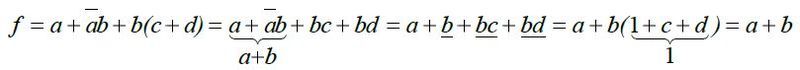
Příklad 4:

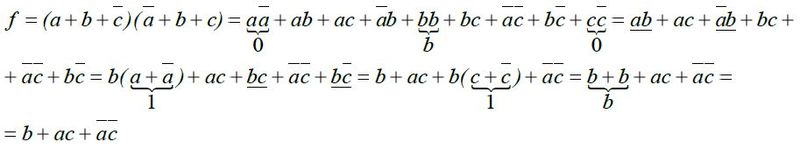
Příklad 5:

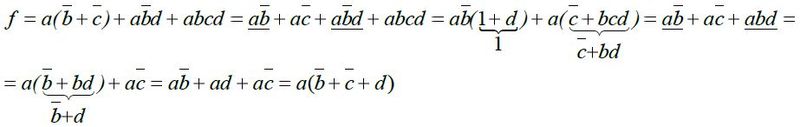
Příklad 6:

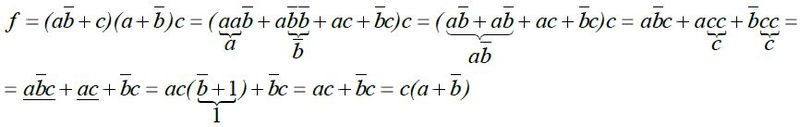
Jak je z ukázek patrné, algebraická minimalizace je poměrně pracná a není příliš vhodná pro složitější funkce více proměnných.

Minimalizace výrazů s využitím Karnaughových map

Karnaughovy mapy pro nás zatím představují nástroj pro grafické vyjádření logických funkcí. Hlavní význam map však spočívá v použití při jejich minimalizaci. To je umožněno základní vlastností Karnaughových map – totiž že se dvě sousední pole se liší v hodnotě pouze jedné proměnné.

Připomeňme, že sousední pole jsou ta, která se dotýkají hranou, svislou či vodorovnou, a rovněž pole na protilehlých okrajích mapy:

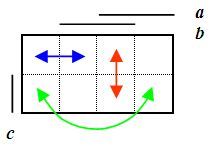
Obr. 1: Sousední pole

Princip minimalizace pomocí map je následující: Obsahuje-li dvojice sousedních polí mapy logické 1, pak jim odpovídající součinové termy se liší pouze negací jedné logické proměnné. Tuto dvojici součinových termů lze nahradit jediným s počtem proměnných o jednotku menším tak, že se z obou vyloučí ona proměnná, která se liší v použití operace negace, podle zákona vyloučeného třetího: a + ā = 1.

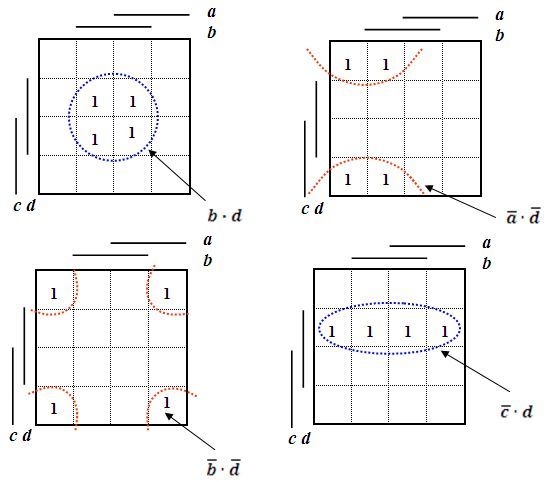
Obr. 2: Náhrada sousedních polí

Celý postup lze algoritmizovat s tím, že nebudeme hledat pouze dvojice sousedních polí obsahující logické 1, ale celé oblasti s počtem sousedních polí rovným mocnině dvou.

1. Hledáme minimalizační smyčky, tj. takové oblasti mapy, které obsahují 2^N polí s funkční hodnotou rovnou logické 1, přičemž každému poli přísluší v této smyčce N polí sousedních (neboli všechny „1“ uzavřeme do smyček ve tvaru čtverce či obdélníka o hranách délky 1, 2, 4, 8…)
2. Snažíme se získat co nejmenší počet co největších minimalizačních smyček, které zahrnou všechna pole s funkční hodnotou logické 1.
3. Minimalizační smyčky se mohou překrývat.
4. Každá minimalizační smyčka generuje součinový term pouze těch proměnných, které mají pro všechna pole dané smyčky stejnou logickou hodnotu (a tedy je-li některá ze společných proměnných nulová, píše se s negací).
5. Nakonec všechny součinové termy svážeme logickým součtem.

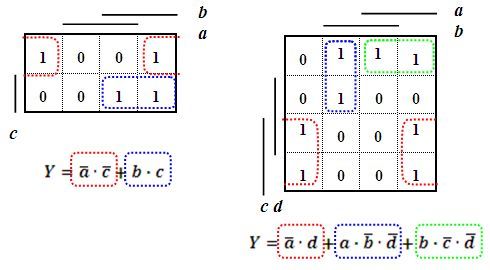
Obr. 3: Minimalizace logických funkcí

Pokrytí mapy minimalizačními smyčkami není jednoznačné, avšak různá pokrytí vedou na analogické struktury minimalizovaného výrazu.

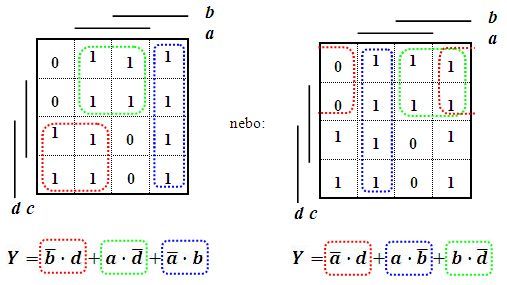
Obr. 4: Analogické minimalizované výrazy

V případě, že počet sousedních polí není roven některé mocnině dvou, je třeba danou oblast mapy pokrýt větším počtem minimalizačních smyček.

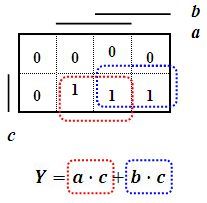
Obr. 5: Minimalizace, kdy počet polí s hodnotou logické 1 není roven mocnině dvou

Je-li logická funkce neúplně zadaná, tedy obsahuje-li pole s nedefinovanou hodnotou (označená symbolem „X“), pak při minimalizaci se tato nedefinovaná pole doplní takovou funkční hodnotou, která zjednoduší výslednou funkci. V následující úloze vede náhrada všech X jedničkami v obou minimalizačních smyčkách k eliminaci nejvyššího možného počtu proměnných.

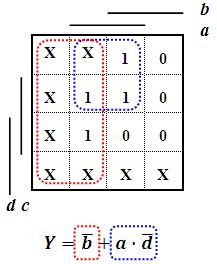
Obr. 6: Náhrada pole s nedefinovanou hodnotou

Posledním krokem při minimalizaci bývá vytýkání logických proměnných před závorku, čímž lze získat absolutně minimální formu logické funkce.

Logický systém obvykle zpracovává několik logických funkcí. Karnaughovy mapy však neumožňují provést exaktní skupinovou minimalizaci. Tu lze provést pouze intuitivně z několika map pro jednotlivé logické funkce s cílem minimalizovat spotřebu realizačních prvků logických obvodů. Postupujeme tak, že se ve všech mapách snažíme hledat společné minimalizační křivky, které generují tzv. skupinové implikanty.

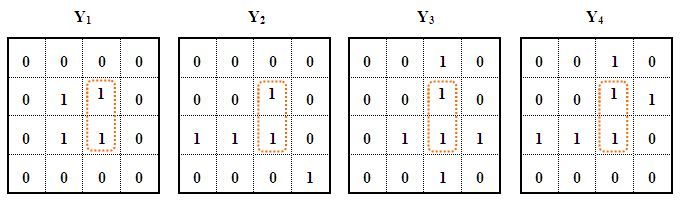
Obr. 7: Skupinová minimalizace

Metoda minimalizace výrazů s využitím Karnaughových map je velmi efektivní pro logické výrazy, či skupiny výrazů, obsahující nejvýše pět logických proměnných. Při vyšším počtu proměnných se však výhody tohoto postupu vytrácejí a je třeba volit jiný postup minimalizace, například metodu Quine – McCluskey.

Zdroje

• HORKÝ, Miroslav. Minimalizace logických funkcí [online]. [cit. 2014-8-7]. Dostupný na www: https://www.vutbr.cz/www_base/zav_prace_soubor_verejne.php?file_id=13493

Obrázky

• Obr. 1, 2, 3, 4, 5, 6, 7: Archiv autora.